Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 36

Таким образом, доходность к погашению будет найдена с учетом возможности реинвестирования получаемого дохода в течение года из следующего уравнения:

.

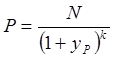Вычислим сначала покупную цену облигации, перемножив курс на номинальную стоимость: руб. Общий доход за 1,5 года по этой облигации составит 2 500–2 250=250 руб. Доходность к погашению определяется из решения следующего уравнения:

;

;

;

.

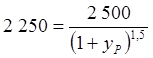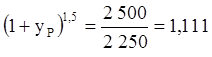Итак, доходность к погашению составляет 7,28% годовых. Это означает, что альтернативно инвестор мог бы, например, поместить 2 250 рублей на депозит под 7,28% годовых сроком на полтора года на условиях ежегодного начисления процентов. Тогда с учетом капитализации процентов в конце 1-го года хранения и начисления процентов в конце срока инвестор получил бы в результате 2 500 рублей. Сравнивая доходность к погашению данной облигации со ставкой процента, действующей в данный период на денежном рынке, инвестор может оценить, стоило ли инвестировать средства в эту ценную бумагу. Эта операция будет оправданной только, если рыночная годовая эффективная ставка процента не меньше 7,28%.

Задача 5

Определите теоретическую рыночную цену купонной облигации номинальной стоимостью 2 500 рублей, эмитированной сроком на  2 года, по которой  ежегодно выплачивается купонный доход в размере 10% от номинала, если годовая эффективная ставка процента равна 11%.

Приобретая такую облигацию в момент эмиссии, владелец обеспечивает себе в конце первого и второго года выплаты в размере  руб., а также при наступлении срока погашения ему будет выплачена номинальная стоимость облигации в размере 2 500 рублей. Расходы на покупки и ожидаемые доходы от владения облигацией можно представить в виде схемы:

                                                                              2500

250                                250

1 год

P=?

Теоретическая стоимость облигации в момент эмиссии представляет собой сумму ожидаемых выплат, приведенных к начальному моменту времени, то есть дисконтированных с применением рыночной ставки процента. Она называется также «внутренней» или «справедливой» рыночной ценой. При приведении будущих доходов к настоящему моменту времени используют также название «современная», «настоящая» или «текущая» стоимость облигации.

Из данного определения следует:

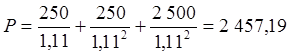 руб.

Таким образом, перспектива получения трех тысяч рублей (2 купона по 250 рублей плюс номинал облигации 2 500 рублей) в течение двух лет оценивается в 2 457,19 рублей, что и определяет теоретическую рыночную стоимость данной облигации в момент эмиссии.

Задача 6

Определите формальную рыночную цену купонной облигации номинальной стоимостью 2 500 рублей, эмитированной сроком на  2 года, по которой по истечении каждого квартала выплачивается купонный доход в размере 2,5% от номинала, если годовая эффективная ставка процента равна 11%.

Приобретая такую облигацию в момент эмиссии, владелец обеспечивает себе в течение двух лет ежеквартальные выплаты в размере  руб., и при наступлении срока погашения ему будет выплачена номинальная стоимость облигации в размере 2 500 рублей. Схема денежных потоков в данном случае выглядит следующим образом:

                                                                              2500

62,50                                                    62,50

P=?

При определении стоимости ценных бумаг предполагается возможность инвестирования промежуточных доходов, т.е. вложения их в другие ценные бумаги или предоставления их в кредит под такие же проценты. Тем самым учитывается разная ценность во времени одних и тех же номинальных сумм. На основе схемы денежных потоков составим уравнение, где в левой части будет стоять искомая цена облигации, а в правой – все будущие доходы ее владельца, приведенные к настоящему моменту времени:

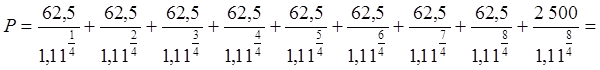
=2474,46 руб.

Таким образом, несмотря на то, что сумма номинальных доходов по этой облигации с восемью купонами такая же, как и в предыдущей задаче для облигации с двумя купонами, рыночная цена этой облигации выше, так как выплаты осуществляются раньше.