Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 11

Задача 9

Бабушка оставила студенту наследство в размере 100 000 рублей с условием хранить его на срочном вкладе в Сбербанке. Студент открыл на эту сумму вклад сроком на 6 месяцев под 9% годовых, и с тех пор по завершении очередного срока вклада снимал на свои нужды 5 000 рублей и переоформлял вклад. На сколько лет хватит этих денег студенту?

Точный ответ потребовал бы учесть дату открытия вклада, что в свою очередь повлияло бы на количество дней в каждом полугодии. Кроме того, в день переоформления вклада проценты начисляться не будут, так что два дня в году не будут входить в срок, используемый для начисления процентов. Однако, сделав некоторые упрощающие предположения, можно найти приближенное решение этой задачи с достаточной степенью точности

Будем считать, что в году два полугодовых срока, и при начислении процентов дни переоформления договора  не пропадают. Обозначим искомое число периодов (полугодий) как t. За каждое полугодие проценты будут начисляться по ставке, исходя из расчетной годовой ставки 9%. На конец первого полугодия сумма вклада составит

руб.

Эта сумма будет уменьшена на 5000 руб., так что базой для следующего начисления процентов будет 99 500 рублей. На конец второго полугодия вклад возрастет до

 руб.

И так далее в течение t полугодий до тех пор, пока сумма вклада не будет исчерпана. Таким образом, на первоначальную сумму 100 000 руб. начисление и капитализация процентов будут произведены t раз. Если бы студент не снимал ежемесячно по 5 000 рублей, то на конец t-го полугодия его состояние равнялось бы  руб.

В то же время, снимая первую сумму 5 000 рублей, вкладчик теряет и проценты за (t-1) полугодий; снимая вторую сумму, он теряет проценты за (t-2) полугодия и так далее. Лишь последняя снятая со счета сумма не могла принести ему процентных доходов. Все снятые суммы и теряемые проценты с этих сумм составляют ряд с числом членов t:

.

Разность между исходной суммой с начисленными процентами и суммой этого ряда и составит конечную величину вклада:

.

Вынесем общий множитель 5 000 за скобки. В квадратных скобках останется сумма геометрической прогрессии с числом членов (t-1), первый член которой равен 1, а знаменатель (1+i₁). Подставив значение i₁=1,045, получим:

.

Составим уравнение, решив которое относительноt, можно будет узнать, на сколько студенту хватит его состояния, то есть, через сколько полугодий оно станет нулевым. Для этого проведем преобразования и прологарифмируем обе части уравнения:

;

;

;

;

;

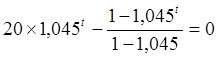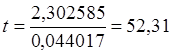полугодия, или 26,16 года.

Имитация процесса на компьютере в таблице Excel показывает, что на конец 53-го срока сумма вклада уже не позволяет снять 5 000 рублей, несмотря на начисленные за этот срок проценты.

Если начислять проценты абсолютно точно, в предположении, например, что вклад открыт 31 декабря 2001 г., то с учетом даты открытия вклада, фактора високосных лет и потери процентов в день переоформления вклада, результат будет отличаться, хотя и незначительно, как видно из следующей таблицы: