Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 41

              1250         1250      1250        1250                                                

                                                                                                                                  t

6 мес.                                                                                                                 

       P₁=?

От этой схемы нужно перейти к схеме ежегодной выплаты дивидендов, то есть заменить все выплаты внутри одного года одной выплатой в конце года. Сумма полугодовых дивидендов по 1250 рублей, приведенных к концу года с помощью коэффициентов наращения, и составит величину эквивалентного годового дивиденда D₁.

D₁                          D₁      

 

1250      1250        1250         1250

1 год.                                                                                                        t

       P₁=?

В коэффициенте наращивания для первого полугодового дивиденда используется полугодовая ставка процента, а второй дивиденд выплачивается в конце года и поэтому приводится к этому моменту с коэффициентом 1. Таким образом, эквивалент годового дивиденда равен

 руб.

Таким образом, акция с ежегодной выплатой 2 566,96 рублей в качестве дивиденда будет иметь такую же стоимость, как и акция с полугодовой выплатой 1 250 рублей. Теоретическая цена такой акции будет равна

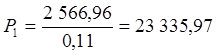 руб.

Аналогично найдем величину эквивалентного годового дивиденда D₂ для второй акции. По этой акции ежеквартально выплачивается 0,025×25 000=625 руб. Схема выплат по этой акции представляется графически следующим образом:

D₂                          D₂      

 

625   625   625    625          

1 квартал                                                                                                        t

       P₂=?

Поэтому в коэффициентах наращения используется ставка процента за 1, 2 и 3 квартала.

 руб.

Поскольку при более частых выплатах время ожидания дивиденда сокращается, то получаемые дивиденды могут быть реинвестированы раньше – уже начиная с начала второго квартала, что обеспечит и более раннее поступление доходов от этих инвестиций в соответствии с рыночной ставкой процента. Поэтому и размер годового дивиденда, эквивалентного четырем квартальным выплатам, оказался больше, чем для первой акции. Соответственно, и теоретическая цена второй акции будет больше, чем первой:

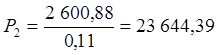 руб.

Примечание. Сопоставимость исходных данных можно обеспечить и иначе: перейдя от годового исчисления ставки процента к полугодовому и квартальному.

При годовой эффективной ставке процента r= 0,11, ставка за полгода составит r_п/г=, а за квартал r_кв= .

Тогда стоимость акций можно рассчитать по известной формуле, прямо используя размер полугодового и квартального дивидендов:

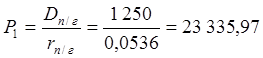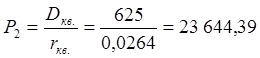 руб.

 руб.

ЗАДАЧА 4

Как меняется во времени теоретическая рыночная цена акций из задачи 3? Постройте график.

В период между выплатами дивидендов цена акции колеблется, возрастая до своего максимального значения к моменту выплаты и резко падая сразу после выплаты дивиденда до минимального значения. Минимальные значения цен – цены за период до выплаты очередного дивиденда – уже найдены в предыдущей задаче.

 руб.

 руб.

Непосредственно перед выплатой дивиденда акцию можно будет продать по максимальной цене, которая больше минимальной на величину дивиденда:

 руб.

 руб.

Таким образом, при одинаковой сумме номинальных выплат в течение года рыночная стоимость акции с меньшей частотой выплат колеблется в бóльших пределах, что показано на графике:

P

                           

24585,97

24269,39

23644,39

23335,97

время

1 год

Примечание. Цены акций колеблются в постоянном интервале от P_min до P_max, так как по данным акциям не запланирован рост дивидендов. Если бы такой рост ожидался, то значения P_min и P_max тоже возрастали бы.

ЗАДАЧА 5