В данной задаче первоначальный график платежей заменяется новым, который должен гарантировать кредитору точно такой же доход, как и при возврате кредита по первому графику. Суммы погашающих платежей и по первому, и по второму графику с учетом фактора времени должны дать одинаковый результат. В этом и состоит условие финансовой эквивалентности различающихся схем платежей. Это условие обеспечивается применением единой годовой эффективной ставки процента для соизмерения разновременных денежных сумм. Построим временную диаграмму для первой схемы:
![]() Q
Q
1 месяц
1,5 1,5 1,5 1,5 1,5 1,5 1,5 1,5 1,5 1,5
Временная диаграмма нового графика платежей:
Q
![]()
20 дней 1 месяц
P1P2P3P4P5P6P7P8P9P10
Найдем задолженность фирмы на начало периода:
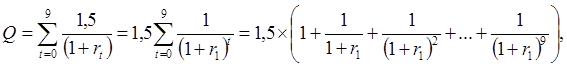
где rt – ставка процента за период.
Ставка процента за месяц при годовой эффективной ставке 18% равна
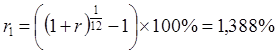 .
.
Используя известную из курса школьной математики формулу, найдем сумму геометрической прогрессии с числом членов 10:
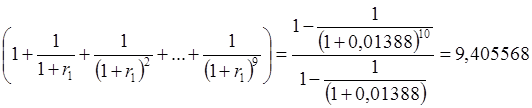 .
.
Отсюда Q=1,5´9,405568=14,108351 млн. руб.
В соответствии с новым графиком эта задолженность должна быть погашена десятью равными платежами, первый из которых выплачивается спустя 20 дней, а последующие – ежемесячно. Запишем уравнение эквивалентности :
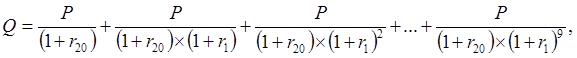
где r20– ставка процента за 20 дней, r1– ставка процента за месяц.
Найдем ставку процента за 20 дней:
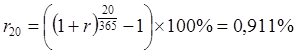 .
.
Перепишем уравнение:
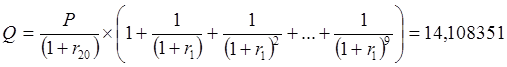 .
.
Сумма ряда уже подсчитана, находим размеры ежемесячных выплат:
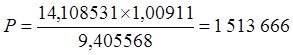 руб.
руб.
Таким образом, выплачивая как по 1 500 000 руб. по 1-ым числам в течение 10 месяцев, так и выплачивая 1 513 666 руб. по 20-ым числам, должник обеспечивает кредитору доходность на уровне 18% годовых.
задача 11.
Фирме X была предоставлена кредитная линия на 1 млн. рублей – в течение 5 месяцев по 1-м числам она брала в банке по 200 тыс. руб. Погашение долга предусматривалось тремя равными ежемесячными платежами ровно через 4 месяца после получения последних 200 тысяч. Найдите величины этих платежей, если для соизмерения денежных сумм во времени используется годовая эффективная ставка 13%?
Построим временную диаграмму платежей
![]() 200 200 200 200 200
200 200 200 200 200
t
4 мес.
P1= P2= P3=?
Запишем условие эквивалентности получаемых в кредит и возвращаемых денежных сумм с учетом фактора времени, приводя платежи к моменту окончательного погашения кредита с помощью множителей наращения. Наращение денежных сумм осуществляется по действующей на рынке ставке процента за соответствующий период в месяцах.
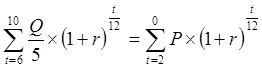 .
.
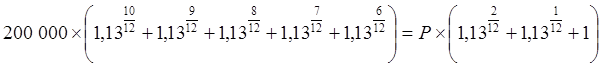 .
.
За первую сумму 200 000 руб. заемщик должен заплатить по ставке за 9 месяцев, за последующие – по уменьшающейся ставке за 8,7, 6 и 5 месяцев. Левая часть уравнения дает сумму, которую заемщик вернул бы в случае единовременного возврата кредита спустя 10 месяцев после получения первых 200 тысяч рублей.
Эта сумма равна 200 000×5,425=1 085 002,35 руб.
В правой части уравнения записано, что три равных платежа должны обеспечить погашение эквивалентной суммы при приведении к концу периода. Из записанного уравнения находим величины этих платежей.
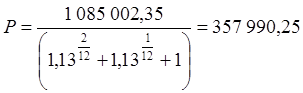 руб.
руб.
Таким образом, фирма должна выплатить три раза по 357 990 руб. 25 коп.
задача 12
Единовременно полученный кредит сроком на 3 года погашался в течение этого срока ежемесячно равными суммами. Для соизмерения денежных сумм во времени использовалась годовая эффективная ставка R. После совершения последнего, 36-го платежа, заемщик обнаружил, что в сумме он заплатил банку ровно в 1,5 раза больше, чем брал у него взаймы. Каково было значение годовой эффективной ставки?
Временная диаграмма платежей выглядит следующим образом:
![]() Q
Q
36 мес.
t
PPPP. . .PP
Из условия задачи следует, что сумма платежей P, приведенных к моменту выдачи кредита с помощью коэффициентов дисконтирования, равна величине кредита Q, а по номиналу в полтора раза превышает его. Эти соотношения дают систему из двух уравнений:
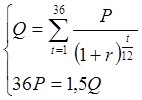
Выразим P через Q (то есть,![]() )
и подставим в первое уравнение:
)
и подставим в первое уравнение:
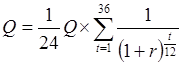 .
.
Отсюда:
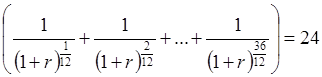 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.