Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 21

И если все банки сохранятся, то вкладчик получит максимально возможную сумму 125 000 рублей.

P{1111111111}=0,95¹⁰=0,5987.

Таким образом, при выборе Стратегии 10 вероятность получить не менее 100 000 рублей (т. е. вероятность разорения не более двух банков из десяти) составляет

P(Z)= 0,5987+0,2836+0,0746=0,9885.

Достигнутый уровень надежности недостаточен. Следовательно, следует разместить средства в пятнадцати банках, т. е. перейти к Стратегии 15.

Стратегия 15. В этом случае допустимо банкротство трех банков. Число событий, благоприятных для вкладчика, возрастает до четырех. Это: 1) сохранение всех банков; 2) банкротство одного банка; 3) двух банков и 4) трех банков. Тогда вероятность разорения не более трех банков из пятнадцати равна

P(Z)= 0,95¹⁵+0,95¹⁴×0,05×10+0,95¹³×0,05²×+0,95¹²×0,05³×=

=0,4633+0,3658+0,1348+0,0307=0,9945.

Теперь вероятность сохранить вложенные средства составляет 99,45%.

Валютные операции

задача 1

Ожидаемый в течение года рост курса доллара составляет 10%. В обменных пунктах банков цена покупки на 3 процентных пункта ниже цены продажи (включая налог). Такой же эта разница останется и в перспективе. Какой должна быть годовая эффективная ставка по рублевым вкладам, чтобы имеющему доллары и нуждающемуся через год в долларах выгоднее было не хранить наличную инвалюту, а обменять ее на рубли, открыть рублевый счет, а через год сделать обратный обмен?

Обозначим курс продажи К_прод. Тогда курс покупки К_пок = 0,97 К_прод. Пусть наличная денежная масса в начале года составляла D долларов. Требуется сравнить результаты альтернативных стратегий: а) хранения наличной валюты и б) конвертирования валюты с хранением на рублевом депозите в течение года.

В первом случае номинальная сумма сбережений в долларах не изменится через год и останется равной Dдолларов. Во втором случае, если гражданин имел D долларов, то продав их в начале года по курсу покупки валюты банком, получит

 руб.

Положив эту сумму на  срочный депозит под i% годовых, через год гражданин снимет со счета сумму, равную

 руб.

Затем на эту сумму гражданин купит доллары по курсу продажи, возросшему за год на 10% и получит

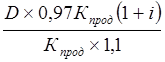 долл.

Если результат данной операции даст больше, чем D долларов, то вторая стратегия является предпочтительной. Запишем это условие в виде неравенства:

;

.

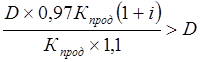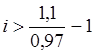Решив неравенство относительно неизвестной i, получаем искомое значение процентной ставки по рублевым депозитам:

i>13,402%.

Если ставка процента строго равна 13,4021%, то результат применения обеих стратегий идентичен. Если же ставка будет выше найденного значения, то выгоднее будет конвертировать валюту в рубли, поместить на депозит и совершить обратное конвертирование в конце года.

задача 2

Пусть сегодня в обменных пунктах российских банков цена покупки и доллара, и евро на 3 процентных пункта меньше цены продажи. Такой же эта разница сохранится и в будущем. Ожидается с большой вероятностью, что ежемесячно в течение длительного времени курс евро по отношению к доллару будет возрастать на 0,4%. Цены покупки и продажи обеих валют будут изменяться такими же темпами, как и биржевые курсы. Гражданин имеет доллары и нуждается в перспективе в долларах Определите, целесообразно ли обменять их на евро, и на какой период запланировать обратный обмен.

У гражданина две альтернативных стратегии. Первая состоит в том, чтобы хранить доллары. Вторая стратегия состоит из следующих действий:1) в начале месяца продажа долларов за рубли по курсу покупки  и покупка на эту сумму евро по курсу продажи , и 2) в конце месяца обратная операция. Для выбора лучшего из альтернативных вариантов требуется определить, принесет ли вторая стратегия больший результат, чем первая.

Курсы покупки и продажи связаны следующими соотношениями:

 = 0,97;

 = 0,97.

Разница между курсами покупки и продажи, выраженная в процентах, называется маржа. В данном случае маржа равна 3%.