Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 20

Пусть событие Z, состоит в том, что по истечении года вкладчик получает сумму, не меньшую первоначальной. (W₁≥100 000 руб.). Пусть стратегия N состоит в открытии N вкладов

Стратегия 1. Если вкладчик откроет только один вклад, то из двух возможных исходов его устроит единственный, при котором он получает максимальную сумму W₁=100 000×1,25=125 000 руб. Для этого банк не должен разориться. Но вероятность этого события {1} всего 95%:

P{1}=1-0,05=0,95=P(Z).

Стратегия 2. Если средства разделить между двумя банками, то вкладчик может: а) потерять все деньги; б) получить только половину с процентами за год; и в) вернуть все деньги с процентами. Вновь вкладчика устраивает только последнее событие (W₁=2×50 000×1,25=125 000 руб.), а вероятность такого исхода (событие {11}) меньше по сравнению со Стратегией 1:

P{11}=0,95×0,95=0,9025=P(Z).

Очевидно, что если продолжать дробить вклады, то вероятность сохранения всех банков (событие, которое требуется для получения 125 000 рублей) будет снижаться, до тех пор, пока не появится хотя бы еще одно событие,  которое устроило бы вкладчика.

Стратегия 5. Если вкладчик распределит свои средства в пяти банках, то его устроит уже два исхода:

1) если ни один банк не разорится, то клиент получит 125 000 рублей с вероятностью

P{11111}=0,95⁵=0,7738;

2) если разорится один из пяти банков, то вкладчик получит 100 000 рублей (W₁=4×25 000×1,25=100 000 руб.). Поскольку разориться может любой из пяти банков, то таких вариантов пять, а вероятность данного события равна

P{11110}=0,95⁴×0,05×5=0,2036.

Реализация любого из событий {11111} и {11110} гарантирует вкладчику как минимум сохранение вложенных средств, Следовательно, сложение вероятностей этих двух событий дает вероятность события Z:

P(Z)= P{11111}+ P{11110}=0,9774.

Вероятность сохранения капитала резко выросла, но если мы дальше будем дробить вклады, то она будет падать (сравните результат Стратегии 2 и Стратегии 1). Для того, чтобы не просчитывать все стратегии, требуется найти минимальный шаг проверки, то есть определить на сколько нужно увеличить число вкладов для того чтобы число благоприятных исходов выросло на единицу. Очевидно, что чем больше вкладов, тем больше будет случаев, когда вкладчика устраивают случаи с банкротством некоторых банков (разумеется, при условии, что проценты, начисленные по сохраненным вкладам, смогут компенсировать потерю некоторых вкладов в банках-банкротах). Запишем это условие.

Если из общего числа вкладов n инвестор теряет b вкладов в разорившихся банках, то у него остается (n-b) благополучных вкладов, по которым будут начислены проценты исходя из годовой эффективной ставки r. В результате капитал возрастет в (n-b)×(1+r) раз. В расчете на общее число вкладов средний результат хранения денег должен быть не менее 100%. Это и будет означать сохранение капитала в целом:

.

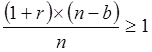Очевидно, что приемлемое число вкладов будет зависеть от допускаемого числа банкротств и от ставки процента:

.

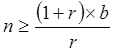Если мы допускаем банкротство одного банка, то должны разместить средства, по крайней мере на пяти счетах (Стратегия 5):

.

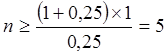Стратегия 10. Если мы допустимо банкротство двух банков, то следует разместить средства на десяти счетах:

.

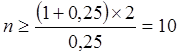Действительно, по мере увеличения числа вкладов от 5 до 10, вероятность сохранения денег будет падать. Но когда капитал  будет размещен на десяти счетах (Стратегия 10) то вкладчика устроит даже разорение двух банков. Тогда он получит с учетом начисленных процентов свои 100 000 рублей(W₁=8×10 000×1,25=100 000). Разориться могут любые два банка из 10. Число таких комбинаций равно 45 (). Отсюда имеем вероятность разорения двух банков при сохранении восьми остальных:

P{1111111100}=0,95⁸×0,05²×45=0,0746.

Кроме того, если разорится только один банк, сумма на конец года составит 112 500 рублей (W₁=9×1000×1,25=112 500).

P{1111111110}=0,95⁹×0,05×10=0,3151.