Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 28

Следовательно, выплачивая ежемесячно по 200 000 руб. в течение пяти месяцев, в сумме можно погасить кредит, равный 944 068,74 руб. Этого недостаточно, чтобы вернуть 1 миллион рублей. Значит, пятый платеж должен быть больше 200 000 руб. на неизвестную величину ΔP₅. Перепишем исходное уравнение:

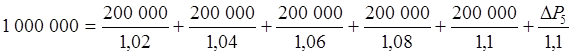
Отсюда ΔP₅=1,1´(1 000 000-944 068,74)=1,1´55 931,26=61 524,39 руб.

Таким образом, последний платеж P₅ должен быть равен 261 524,39 руб. Найденная нами величина ΔP₅ – это стоимость кредита на сумму один миллион сроком 5 месяцев, рассчитанная методом дисконтирования. Таким образом,

I= ΔP₅=61  524,39 руб.

Задача 6

Для условий задачи 5 постройте временные диаграммы потоков  платежей и объясните, почему расчет номинальной стоимости кредита по актуарному методу, методу торговца и методу дисконтирования дал разные результаты

Для ответа на поставленный вопрос нужно для каждого метода записать стандартное уравнение эквивалентности, то есть уравнение, показывающее, что настоящая стоимость кредита равна сумме всех погашающих платежей с поправкой на время. Такое уравнение выписывается на основании графической схемы двустороннего потока платежей во времени для данных условий кредита.

а) Расчет стоимости кредита по актуарному методу можно представить как серию последовательно  выданных пяти кредитов разного объема сроком на 1 месяц.

Первый кредит 1млн. руб., взят на 1 месяц, а по истечении срока кредита в его погашение перечислено только 200 000 руб. Тогда оформляется  новый кредит сроком на 1 месяц, равный остатку задолженности и сумме начисленных процентов. По окончании второго месяца срок второго кредита истекает, но в счет уплаты поступает только 200 000 руб. Поэтому на оставшуюся сумму с процентами берут новый кредит сроком на один месяц, и так далее в течение пяти месяцев. Пятый платеж полностью возмещает остаток задолженности с процентами

Q₁.=1 млн.  Q₂

Q₃              Q₄                

                                                                                    Q₅

                  200000      200000         200000         200000            P₅

Запишем условия эквивалентности для каждого кредита, приводя суммы на начало соответствующего месяца, используя в качестве нормы дисконтирования месячную ставку процента. Величина заключительного платежа P₅ находится в результате последовательного расчета кредитов Q₂, Q₃, Q₄ и Q₅. Зная размер первого кредита Q₁, находим сначала величину Q₂, затем Q₃, и так далее до последнего платежа.

;

                              ;

                                                      ;

                                                                                 ;

                                                                                                            .

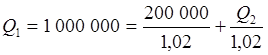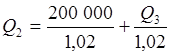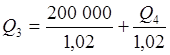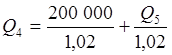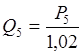Общее уравнение эквивалентности будет следующим:

.

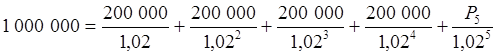Отсюда находим  пятый платеж:

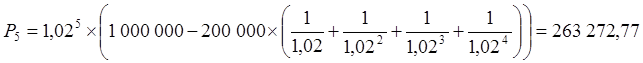 руб.

б) Идея метода торговца  состоит в том, чтобы сумма платежей с начисленными на них процентами в конце срока кредита сравнялась с суммой кредита с начисленными на нее процентами. Другими словами, происходит наращение и суммы задолженности, и сумм погашающих выплат с использованием ставки процента за соответствующий срок (от 1 до 5 месяцев).

Q

      200000    200000       200000          200000            P₅

Приводя датированные платежи к концу срока кредита, получаем следующее уравнение эквивалентности:

.

Отсюда находим величину последнего платежа:

 руб.

в) Временная схема для метода дисконтирования отличается от предыдущей только тем, что все денежные суммы приводятся к началу периода, то есть, дисконтируются с использованием ставки процента за соответствующий срок (от 1 до 5 месяцев).

Q

         200000      200000      200000      200000   P₅

Запишем уравнение эквивалентности денежных сумм во времени:

.

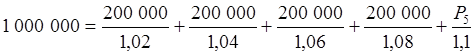Отсюда:

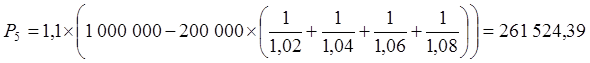 руб.