Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 24

б) Если при расчете процентов используется годовая эффективная ставка, это означает, что используется техника сложных процентов, так как формула сложных процентов учитывает возможность реинвестирования (капитализации) процентов, получаемых кредитором. Годовая эффективная ставка обозначается r.

Требуется рассчитать ставку сложного процента за 4, 5 месяца r_4,5. Перейдем сначала от годовой эффективной ставки r к ставке за месяц r₁. Запишем формулу сложных процентов как уравнение с неизвестной ставкой за месяц r₁, двенадцатью периодами начисления процентов и известной годовой ставкой r=14%.

.

Отсюда рассчитаем ставку сложного процента за месяц:

.

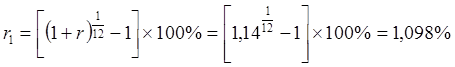Соответственно, ставка процента за 4,5 месяца составит

.

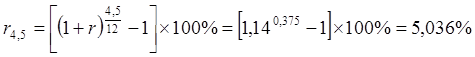Величина погашающего платежа равна

 руб.

Стоимость кредита, как разница между выданной и возвращенной суммами, составит I_4,5 = 682 735,8–650 000=32 735,8 руб.

Стоимость кредита в случае (а) равна 0,0525×650 000=34 125 руб., а в случае (б) – 0,05363×650 000=32 735,8 руб. Следовательно, использование техники простых процентов выгодно для кредитора, а для заемщика кредит обходится дешевле при использовании метода сложных процентов.

Примечание. Из формул сложных и простых процентов с очевидностью следует, что различия в стоимости кредита возникают при сроках меньше и больше одного года. Если же срок кредита равен одному году, то формулы простых и сложных процентов дают одинаковый результат.

Задача 3

Какие суммы должен отдавать заемщик кредитору, если погашение кредита предусматривается двумя равными суммами – соответственно через 2,5 месяца и через 4,5 месяца, при условии, что:

а) расчетная ставка равна 14%, а для соизмерения денежных сумм во времени используется формула простых процентов;

б) годовая эффективная ставка равна 14%,аи для соизмерения денежных сумм во времени используется формула сложных процентов?

Построим временную диаграмму платежей. Полученный кредит 650 000 руб. должен быть возмещен двумя равными платежами P, значение которых предстоит найти.

Q=650000 руб.

2,5                4,5                         t (мес.)

                                                   P=?              P=?

Запишем общее условие эквивалентности выданного кредита и суммы погашающих платежей с учетом изменения стоимости денег во времени.

Если кредит Q погашается серией периодических платежей P, осуществляемых в течение периода t, то сумма этих платежей должна полностью возместить этот кредит. Но платежи осуществляются в разные моменты времени, что делает невозможным их прямое суммирование, то есть суммирование без учета фактора времени. Фактор времени учитывается с помощью множителя дисконтирования 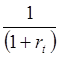 где r_t –действующая на рынке ставка банковского процента за период t. Дисконт или скидка показывает, что будущий платеж всегда имеет меньшую стоимость, чем равный по сумме платеж, осуществляемый в настоящий момент времени. Стандартное уравнение эквивалентности для потока из t выплат записывается следующим образом:

.

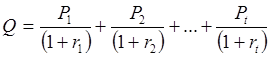а) Для случая простых процентов и двух равных платежей уравнение будет иметь следующий вид:

.

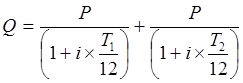Первый платеж отстоит от момента выдачи кредита на T₁= 2,5 месяца и дисконтируется по ставке за 2,5 месяца 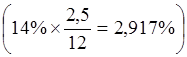. Таким образом, мы учитываем, что возвращаемая сумма P должна обеспечить кредитору доход на уровне рыночной ставки процента. Второй платеж дисконтируется по ставке за T₂=4,5 месяцев .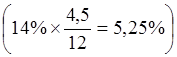

Остается решить уравнение

.

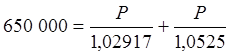Отсюда погашающие платежи составят по 338 228,33 руб. каждый.

б) В случае сложных процентов в уравнении эквивалентности денежных сумм во времени изменится значение ставок за период и вид дисконтного множителя.

.

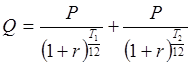Уравнение будет записано следующим образом:

.

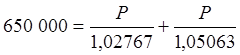Отсюда первый и второй погашающие платежи равны по 337 640,64 руб..

Задача 4

Кредит на сумму 650 тысяч рублей получен на условиях погашения его единовременным платежом через 4,5 месяца и уплаты процентов в момент выдачи кредита. Какую сумму должен будет возвратить заемщик кредитору, и какова стоимость кредита, если: