Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 13

В начале обучения студент открыл депозитный счет на сумму 500 рублей сроком на месяц с автоматической пролонгацией вклада. Расчетная ставка процента 8% в год. В течение 4-х лет студент в день окончания очередного срока вносил на счет по 500 рублей. Уровень инфляции в эти годы составлял 8% в год, ставка процента оставалась неизменной. Счет был закрыт ровно через 4 года после открытия.

А) Какую сумму получил студент на руки?

Б) Какой была реальная ставка по этому вкладу?

В) Рассчитайте реальный эквивалент полученной суммы.

Эта задача, подобно задачам 7 и 9, решается приближенно, в предположении, что месяцы и годы имеют равную продолжительность.

А) За 4 года студент внесет на свой счет 48 раз по 500 рублей, всего – 24 000 рублей. С учетом ежемесячного начисления процентов эта сумма на момент закрытия вклада и составит

W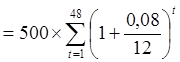=500×(1,00667⁴⁸+1,00667⁴⁷+…+1,00667).

Найдем сумму множителей наращения в скобках, используя формулу геометрической прогрессии:

.

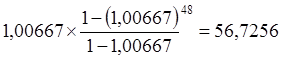Значит, по истечении четырех лет студент получит

W=500×56,7256=28 362,79 руб.

Это – номинальная сумма сбережений студента (без учета снижения покупательной способности денег в ходе инфляции).

Б) Годовая эффективная ставка процента r при расчетной ставке 8% и 12 периодах начисления процентов за год равна

.

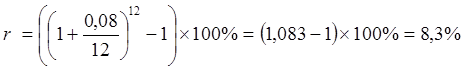С учетом инфляции реальная годовая ставка процента r_g будет равна

.

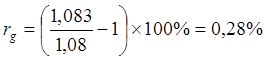Реальная годовая ставка r_g оказалась положительной, несмотря на равенство темпа инфляции и расчетной ставки процента, так как эффективная ставка процента выше темпа инфляции. Следовательно, покупательная способность средств будет не только сохранена, но и приумножена.

В) В этой задаче инфляция дана в годовом исчислении, а пополнение счета и начисление процентов происходит ежемесячно.

Сначала рассчитаем годовой эквивалент двенадцати ежемесячных взносов на депозит. Для этого с помощью множителей наращения 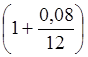 найдем будущую стоимость этих платежей K₁. На конец года эквивалентная сумма составит

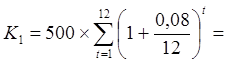500×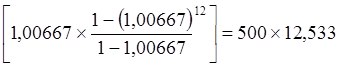=6 266,46 руб.

Следовательно, если учитывать возможность реинвестирования вносимых сумм под рыночную ставку процента, то сумма 6 266,46 рублей, внесенная в конце года, заменяет 12 платежей по 500 рублей, вносимых ежемесячно в начале месяца. Но этот показатель рассчитан без учета инфляции. Найдем реальный эквивалент K_g данной суммы с учетом роста цен за год на 8%:

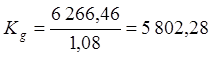 руб.

Теперь мы можем применить найденное выше значение реальной ставки процента к годовому эквиваленту ежемесячных взносов на депозит. Начислим проценты за 4 года хранения:

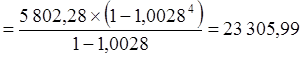 руб.

Таким образом, в реальном выражении (то есть в ценах на момент начала операции) сумма сбережений W_gна конец четвертого года составит 23 305,99 рублей.

Почему эта величина оказалась меньше, чем 24 000 рублей, внесенные в течение четырех лет? Противоречит ли это положительному значению рассчитанной нами реальной ставки процента? Дело в том, что мы учли не только обесценивание денег вследствие инфляции, но и разную стоимость денежных сумм, вносимых в разные периоды времени.

Для сравнения предположим, что 24 000 рублей были внесены единовременно в начале срока хранения. За 4 года вклад возрастет до 24 000×1,000667⁴⁸=33 015,99 рублей. С учетом инфляции реальный эквивалент данной суммы составит  рублей, что превышает начальную величину капитала в 1,0116 раза. Следовательно, за год сумма вклада возрастала в =1,00277 раза, что в точности соответствует реальной годовой ставке 0,28%, которая была рассчитана в пункте Б.

задача 12

Для того чтобы приближенно оценить темп роста инвестиций или капитала, финансисты и инвесторы издавна пользуются эмпирическим «правилом 70» Оно гласит, что «время удвоения капитала (в годах) равно , где i – годовая ставка процента, выраженная в процентах». На чем основано это правило? При каких условиях оно обеспечивает достаточно точную аппроксимацию?