Точный срок ссуды определяется по календарю. При подсчете приближенного срока месяц принимается равным 30 дням, день выдачи и возврата кредита считаются за один день, так что срок кредита равен числу полных месяцев, умноженному на 30 плюс число дней в неполных месяцах плюс один граничный день.
Обозначим величину ссуды – Q,. годовую расчетную ставку процента – i, стоимость кредита, выданного на срок t дней – It.
Точная продолжительность ссуды t равна (359-105)=254 дня, где 359 и 105 – порядковые номера дней 25 декабря и 15 апреля.
Приближенная продолжительность равна 30×7+15+24+1=250 дней.
Рассчитаем стоимость кредита It. , т. е. величину начисленных процентных денег, по трем вариантам.
а) Точные проценты с точным числом дней
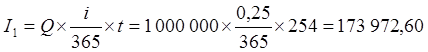 руб.
руб.
б) Обыкновенные (коммерческие) проценты с точным числом дней
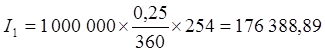 руб.
руб.
в) Обыкновенные (коммерческие) проценты с приближенной продолжительностью ссуды
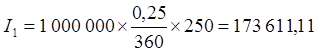 руб.
руб.
Применение второго способа начисления процентов обеспечивает наибольший эффект для кредитора. Разница между наибольшей и наименьшей величиной платы за кредит составляет 176 388,89–173 611,11=2 777,78 руб.
Примечание. Данная финансовая операция также представляет собой пример наращения, т. е. увеличения первоначальной суммы капитала в результате начисления процентов. Величина предоставленной ссуды здесь является настоящей или современной величиной капитала (на момент выдачи ссуды), а будущая величина капитала – это ссуда с процентами.
Умножив современную стоимость капитала на множитель наращения, мы получили его будущую стоимость (на момент возврата ссуды). Величина множителя наращения зависела от применяемого способа начисления процентов и составила 1,173972, 1,176389 и 1,173611, соответственно.
Кредит на сумму 650 тысяч рублей получен на условиях погашения его единовременным платежом вместе с процентами через 4,5 месяца. Какую сумму должен будет возвратить заемщик кредитору, и какова стоимость кредита, если:
а) кредиты на такие сроки предоставляются исходя из расчетной ставки 14% годовых, а для исчисления стоимости кредита используется формула простых процентов;
б) для кредитов на любые сроки используется годовая эффективная ставка – 14%?
Техники начисления простых и сложных процентов различаются используемой базой начисления. В случае простых процентов начисление за любой промежуток времени производится на исходную сумму капитала (по состоянию на начало операции). Таким образом, наращение капитала идет по линейному закону. Если n- - общее число периодов начисления по годовой ставке за весь срок, то исходный капитал W0 за n периодов возрастет до величины Wпо следующей формуле:
![]()
В случае сложных процентов базой для начисления процентов за каждый промежуток времени служит сумма капитала с накопленными на данный момент процентами. Рост капитала происходит по экспоненциальному закону в соответствии с формулой:
![]()
Построим диаграмму поступлений и платежей. По горизонтальной оси отложим промежутки времени между платежами, выше оси отметим поступления на счет заемщика, ниже оси – выплаты со счета заемщика. Все платежи имеют дату и называются датированные платежи. Высота столбиков пропорциональна размеру платежей. Первый платеж осуществляется в нулевой момент времени. Такая диаграмма называется еще «временнáя диаграмма». Обозначим сумму возврата P. Это – будущая стоимость предоставленных в ссуду денежных средств, она включает в себя кредит Q и проценты за 4,5 месяца I4,5.
Q =650000 руб.
![]()
4,5 t (мес.)
P=?
а) При расчете по формуле простых процентов
расчетной ставке i=14% годовых соответствует ставка за 4,5
месяца, равная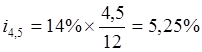 .
.
Возвращаемая сумма должна быть увеличена в соответствии со стоимостью кредита (умножена на множитель наращения 1,0525) и составит
![]() руб.
или
руб.
или ![]() руб.
руб.
Стоимость кредита, как разница между выданной и возвращенной суммами, составит I4,5 = 684 125–650 000=34 125 руб.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.