Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 33

задача 14

Банк А заключил контракт, согласно которому клиент получает ссуду в размере 100 млн. руб. на условиях возврата равными суммами в конце каждого года в течение трех лет, причем на непогашенный остаток ежеквартально начисляются сложные проценты исходя из расчетной ставки 20% годовых. В скором времени банк А получил конфиденциальную информацию о надежности заемщика и решил срочно переуступить этот контракт другому банку Б, который выдает кредиты на тех же условиях, но с ежеквартальным начислением процентов. По какой цене будет продан этот контракт? Будет ли эта сделка выгодной для первого банка?

Прежде всего, нужно определить, какие годовые платежи обеспечивает кредитору А данный контракт. В конце первого полугодия банк начисляет проценты на всю сумму ссуды по ставке, равной 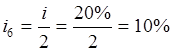 за 6 месяцев. В конце второго полугодия проценты начисляются на ссуду и накопленные проценты по той же ставке, после чего клиент переводит первый погасительный платеж X₁.В конце третьего полугодия снова начисляются проценты на непогашенный остаток кредита, и так далее в течение трех лет. В результате в конце первого года клиент имеет задолженность, равную () млн. руб., в конце второго года –  млн. руб., и в конце третьего года задолженность равняется  млн. руб., что в точности равно величине последнего платежа.

Построим временную диаграмму денежных потоков

X₁                               X₂                             X₃

                                                                                                                                                       t

6 месяцев

Q=100 000 000 руб.

Современная стоимость суммы будущих платежей составляет сумму кредита, что позволяет записать следующее уравнение:

.

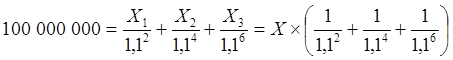Отсюда находим, что кредит будет погашен тремя равными взносами по 48 217 549,88 руб. Иными словами, согласно заключенному контракту, банк А единовременно инвестирует 100 000 000 рублей, что обеспечивает ему в течение трех следующих лет денежный поток номинальной суммой 144 652 649,63 руб.

Когда банк А предлагает банку Б этот контракт, банк Б должен оценить его будущую стоимость исходя из собственных условий. При ежеквартальном начислении процентов на непогашенный остаток ссуды по квартальной ставке  приведенная сумма будущих платежей представляется для банка Б следующим образом: