![]() 2559,01 2562,5
2559,01 2562,5
2539,87 2496,51
2474,46
2477,37
время
Задача 9
Выпущена двухлетняя облигация номиналом 2,5 тыс. рублей. Два раза в год по ней предусмотрены выплаты купона по ставке 5%. Сразу после эмиссии облигация продается по курсу 95. Что лучше предпринять: покупать или продавать эту облигацию, если годовая эффективная ставка процента на денежном рынке составляет 12%?
Для того чтобы оценить, целесообразно ли инвестировать средства в данную ценную бумагу, следует сравнить доходность, обеспечиваемую этой облигацией с доходностью альтернативных инвестиций, доходность которых представлена рыночной ставкой процента (12%). Следовательно, нужно определить доходность облигации к погашению.
Доходность к погашению представляет собой эффективную процентную ставку (в годовом исчислении), дисконтирование по которой приравнивает величину доходов, обеспечиваемых покупкой данной облигации к покупной стоимости облигации. Запишем уравнение, в котором текущая стоимость облигации определяется как сумма купонных выплат и номинала, выплачиваемого при погашении, приведенных к начальному моменту времени с помощью показателя доходности к погашению.
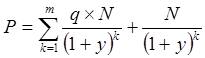 ,
где q – ставка купона, N – номинальная стоимость облигации, y
– показатель доходности к погашению.
,
где q – ставка купона, N – номинальная стоимость облигации, y
– показатель доходности к погашению.
Для того чтобы определить доходность к
погашению, нужно, прежде всего, вычислить покупную цену, перемножив курс на
номинал: 2500*0,95=2375 руб. Купонные выплаты составят ![]() рублей
и будут осуществлены 4 раза за двухлетний период. Кроме того, в конце срока
владельцу будет погашена номинальная стоимость облигации 2500 рублей. Поток
платежей по облигации представляется числовым рядом (-2375; 125; 125; 125;
2625) и может быть представлен в виде графической схемы:
рублей
и будут осуществлены 4 раза за двухлетний период. Кроме того, в конце срока
владельцу будет погашена номинальная стоимость облигации 2500 рублей. Поток
платежей по облигации представляется числовым рядом (-2375; 125; 125; 125;
2625) и может быть представлен в виде графической схемы:
![]() 2500
2500
125 125 125 125
2375
Внутренняя норма доходности этого денежного потока и есть доходность облигации к погашению. Значит, доходность к погашению может быть найдена из решения следующего уравнения:
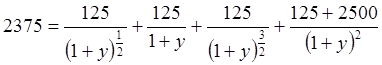 .
.
Задача 10
Выпущена вечная облигация без номинала (консоль), владельцы которой могут ежегодно получать по 2500 рублей. Какой будет ее цена в момент эмиссии, если на рынке ссудного капитала годовая эффективная ставка составляет 11%? Первый доход выплачивается через год, все последующие – с такой же периодичностью.
Вечные облигации (консоли) не имеют конкретного срока погашения. Владелец таких облигаций регулярно получает определенную фиксированную сумму A в течение необозримого периода, как это показано на графической схеме:
![]() A A A A A
A A A A A
t
1 год
P=?
В этом случае денежный поток представляет собой вечную ренту, приведенная стоимость которой и является внутренней стоимостью облигации. Определим современную стоимость всех будущих доходов Ai исходя из существующей годовой эффективной ставки процента r. Имеем уравнение.
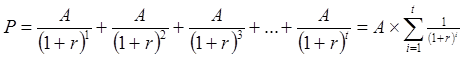 .
.
В его правой части – сумма геометрической прогрессии с бесконечным числом членов. Формула для определения суммы n членов геометрической прогрессии:
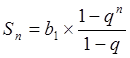 , где b
, где b![]() –
первый член прогрессии, q – знаменатель прогрессии, b
–
первый член прогрессии, q – знаменатель прогрессии, b![]() =
b
=
b![]() q.
В нашем случае первый член b
q.
В нашем случае первый член b![]() =
=
![]() ,
а знаменатель q =
,
а знаменатель q = ![]() .
Подставляя эти значения в формулу, получаем:
.
Подставляя эти значения в формулу, получаем:
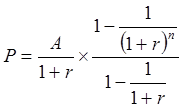 .
.
При n = ¥ знаменатель
дроби 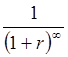 стремится
к бесконечности, а само выражение стремится к нулю, то есть
стремится
к бесконечности, а само выражение стремится к нулю, то есть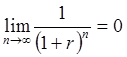 .
Тогда
.
Тогда
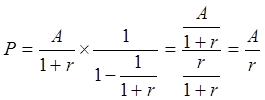
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.