Номинальная стоимость акции служит базой для
расчета дивидендов. Владелец такой акции ежегодно получает в качестве
дивидендов 
руб.
Предполагается, что предприятие-эмитент будет работать стабильно, гарантируя
таким образом выплату дивидендов в течение неопределенно долгого периода
времени. Денежный поток, обеспечиваемый данной акцией, представлен на
графической схеме:
2500 2500 2500 2500 2500
1 год t
P=?
Современная стоимость акции представляет собой сумму бесконечного ряда дивидендов, приведенных к настоящему моменту времени, то есть дисконтированных по рыночной ставке процента. (Точно так же рассчитывается и рыночная стоимость вечной облигации (консоли) с такой же доходностью.) Номинальная стоимость акции в расчете не используется.
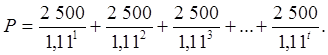
Уравнение рыночной стоимости акции преобразовывается с помощью формулы суммы геометрической прогрессии с бесконечным числом членов t :
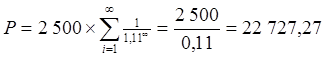руб.
Таким образом, для расчета формальной теоретической стоимости акции P за год до получения очередного дивиденда достаточно знать абсолютный размер ежегодного дивиденда D, и уровень рыночной ставки процента r:
.
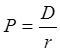ЗАДАЧА 2
На рынке обращаются акции известной фирмы, которая демонстрирует устойчивый рост прибыли в течение ряда лет. Соответственно, фирма гарантирует и ежегодный рост дивидендов на 2% ежегодно. Определите теоретическую рыночную стоимость акции этой фирмы, если дивиденд в размере 2 500 рублей за истекший год уже получен, а до выплат следующего остается ровно год. Годовая эффективная ставка процента на денежном рынке составляет 11%.
Когда фирма работает стабильно, можно ожидать роста дивидендов в будущем. Если ожидается равномерное увеличение суммы выплачиваемых дивидендов с планируемым темпом g, а выплаченный в базисном году дивиденд составил D0, то денежный поток можно представить следующим образом:
D´(1+g)t
D´(1+g)3
D´(1+g)2
D´(1+g)
t
1 год
P=?
При такой схеме выплат известная формула расчета цены акции усложняется.
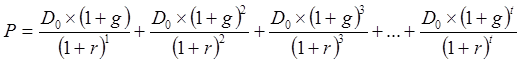, где r - действующая на рынке ставка процента.
Преобразуем формулу:
.
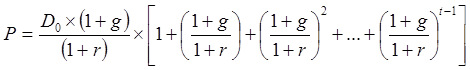В квадратных скобках – сумма геометрической прогрессии
с числом членов t, сумма которой 
,
где b
-
первый член прогрессии, q – знаменатель прогрессии, b
=
b
q.
В нашем случае первый член b =
,
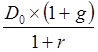а знаменатель q = 
.
Подставляя эти значения в формулу, получаем:
.
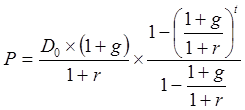Полагая t = ¥ и учитывая, что g<r, получаем, что 
.
Отсюда:
.
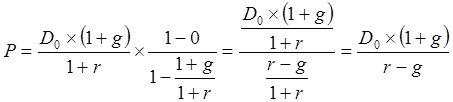Полученная формула называется по имени ее автора моделью Гордона и широко используется для оценки обыкновенных акций крупных и многоотраслевых компаний.
В условиях данной задачи:
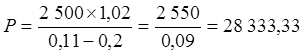руб.
Сравнение с акцией из задачи 1 демонстрирует, что ожидание даже небольшого роста дивидендов заметно увеличивает внутреннюю стоимость акции.
Примечание. Если известен уровень дивидендов, ожидаемых к выплате в ближайшем планируемом периоде (D1), то формула Гордона приводится к следующему виду (при g<r):
.
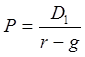ЗАДАЧА 3
На фондовом рынке обращаются два вида акций номинальной стоимостью 25 000 рублей. Акции первого типа предусматривают выплату дивидендов два раза в год в размере 5% от номинала. По акциям второго типа доход выплачивается ежеквартально по ставке дивиденда, равной 2,5% от номинала. Какие акции будут иметь на сегодняшний день бóльшую рыночную стоимость? Годовая эффективная ставка процента на денежном рынке составляет 11%.
В этой задаче ставка процента задана в годовом исчислении, а дивиденды выплачиваются чаще, чем раз в год. Требуется привести исходные данные к сопоставимому виду.
Если решать задачу в годовом исчислении, то требуется знать объем эквивалентных годовых выплат по акциям. По акциям первого типа выплаты дивиденды в размере 0,05×25 000=1 250 руб. выплачиваются по следующей схеме:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.