Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 27

.

Основной долг равномерно возрастает за пять месяцев с 1 миллиона рублей до 1 миллиона 100 тысяч рублей в соответствии с начисленной ставкой процента за 5 месяцев . Первый взнос 200 000 руб. пролежит на депозите 4 месяца, и за этот срок. должнику начислят проценты за 4 месяца в размере: 0,02´4´200 000 руб. = 16 000 руб. На второй взнос будут начислены проценты за три месяца в размере: 0,02´3´200 000 руб. = 12 000 руб. и т.д. На последний взнос проценты не будут начислены.

К моменту выплаты пятого взноса на депозите будет накоплена сумма, равная 4/5 номинальной стоимости кредита и начисленным на него процентам в размере 40 000 руб. В то же время должник обязан выплатить 1 млн. 100 тыс. руб. Вычтя из этой суммы накопленные платежи с процентами, получаем величину заключительного платежа:

P₅ = 1 000 000 ´ (1+0,02´5) – 200 000 ´ [(1+0,02´4) +1+0,02´3) +

+ (1+0,02´2) + (1+0,02´1)] = 1 100 000 – 840 000 = 260 000 руб.

В эту сумму входят последние 200 000 руб. и проценты 60 000 руб.

I=P₅–=60 000 руб.

Стоимость кредита оказалась меньше, чем стоимость, рассчитанная по актуарному методу.

Движение средств в этом случае можно представить как два счета: кредитный и депозитный.

Номер месяца	Кредитный счет		Депозитный счет
	Долг на начало месяца	Долг на конец месяца	На начало месяца	Начисленные проценты	Взнос в погашение основного долга	Платежи с процентами на конец месяца
T	Q	Q´(1+i)	Dt-1+ Pt	Pt-1´i´t	Pt	Dt=Pt-1´i´t+ Pt
1	1 000 000	1 020 000	0	0	200 000	200 000
2	1 020 000	1 040 000	200 000	4 000	200 000	404 000
3	1 040 000	1 060 000	404 000	8 000	200 000	612 000
4	1 060 000	1 080 000	612 000	12 000	200 000	824 000
5	1 080 000	1 100 000	824 000	16 000	200 000	840 000
Последний погашающий платеж (1 100 000-840 000)=						260 000

в) Расчет стоимости кредита по методу дисконтирования предполагает, что кредит Q= 1 млн. руб. представляется как серия из пяти кредитов, взятых в начале периода на разные сроки от одного до пяти месяцев.

                            200 000

Q₁

1

Время, t

                                                      200 000

Q₂

Время, t

…

Q₅

P₅

                                                                                                                                                                   

Время, t

Тогда первый платеж P₁ полностью возмещает первый кредит Q₁, взятый на 1 месяц, второй P₂ идет в погашение второго кредита Q₂, сроком на 2 месяца и так далее, до последнего платежа, стоимость которого предстоит определить.

Q= Q₁+ Q₂+ Q₃+ Q₄+ Q₅

Найдем сначала, какие кредиты Q_t сроком на 1, 2, 3 ,4 и 5 месяцев могут быть погашены платежами P_t по 200 000 рублей.

Каждый платеж P_t включал в себя возмещение основного долга Q_t и проценты за пользование кредитом в течение t месяцев. P_t =Q_t´(1+i´t), где i - ставка процента за 1 месяц. Запишем и решим аналогичные уравнения для всех пяти платежей.

200 000= Q₁´1,02, откудаQ₁==196 078,43 руб.

200 000= Q₂´1,04, откудаQ₂==192 307,69 руб.

200 000= Q₃´1,06, откудаQ₃==188 679,25 руб.

200 000= Q₄´1,08, откудаQ₄==185 185,19 руб.

200 000= Q₅´1,08, откудаQ₅==181 818,18 руб.

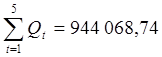 руб.