Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 30

Задолженность клиента перед банком сократилась, и за второй месяц он должен платить проценты с меньшей суммы кредита:

Q₂=Q–Q₁=20 000–3 333,33=16 666,67 руб.

Ставка процента за второй месяц продолжительностью 30 дней составит

.

За второй месяц клиент заплатит в виде процентов

 руб.

Далее начисление процентов производится аналогично. Представим расчеты в виде следующей таблицы:

Номинальная стоимость кредита составила 2 110, 68 руб.

б) Понятие эффективной ставки уже рассматривалось в задаче 6 раздела «Депозитные операции». Применительно к кредиту эффективная ставка показывает стоимость займа одного рубля на год. Это годичная ставка сложного процента, эквивалентная конкретным условиям погашения кредита.

Для измерения эффективной процентной ставки выданный кредит Qинтерпретируется как текущая (приведенная) величина потока погасительных платежей P_i. Под текущей величиной потока платежей понимается сумма всех дисконтированных членов такого потока на “нулевой” момент времени, то есть на момент выдачи кредита.

   Q

P₁          P₂          P₃          P₄          P₅          P₆

Каждый платеж приводится к начальному моменту времени с помощью дисконтного множителя за соответствующий период. Ставка процента, используемая в дисконтном множителе, есть неизвестная эффективная ставка данного кредита. Приравняв сумму кредита и текущую величину потока платежей, дисконтированную по неизвестной ставке r, получаем уравнение, которое нужно решить относительно r.

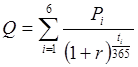, где t_i – период в днях от выдачи кредита до i–го погасительного платежа.

Итак, уравнение эквивалентности:

.

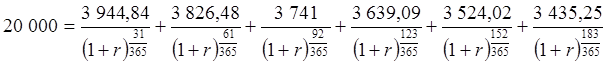Такое уравнение решается в пакете Excel  с помощью функции «Подбор параметра».

Равенство кредита и приведенной суммы платежей достигается при 42,57% годовых.

.

Эффективная ставка данного кредита – 42, 57% годовых. Это значит, что кредитору безразлично – выдать кредит на год под 42,57% годовых на условиях единовременного возврата вместе с процентами, либо выдать кредит на полгода под 36% годовых на условиях ежемесячного возврата равными долями с одновременной уплатой процентов на непогашенную часть основного долга. И в первом, и во втором случае его приведенный (к начальному моменту времени) годовой доход составит 42,57 коп. с каждого ссуженного рубля.

задача 10

Фирма обязана выплачивать 1-го числа каждого месяца полтора миллиона рублей течение 10 месяцев. Замените это обязательство финансово эквивалентным, если сроки всех выплат отодвигаются на 20 дней, а для соизмерения денежных сумм во времени используется годовая эффективная ставка 18%.