Введение в физическую химию формирования текстуры гетерогенных катализаторов (часть III), страница 8

Поэтому в настоящее время  для анализа механизмов  формировании ВСГиз ПСГ приходится использовать менее строгие, как правило, полуколичественные  и зачастую, эмпирические подходы, базирующиеся на общих физико-химических принципах. Используем такой подход для анализа наиболее вероятных процессов, происходящих при конденсации ПСГ в ВСГ и на других стадиях, связанных с образованием и старением осадка, включая фазовые превращения при старении, сушке и термо-обработке.

При формировании ВСГ из ПСГ для обеспечения устойчивости определенных форм ВСГ важнейшее значение имеет согласование электростатических характеристик, размеров и морфологии контактирующих полиэдров. Геометрические факторы упаковки полиэдров подробно рассматриваются в курсах кристаллохимии [[29]^{,[30],[31],[32]}]. Ряд правил для ионных кристаллов, учитывающих геометрические и электро-статические факторы, обобщил или сформулировал в 1929 г. Полинг (см. в [^23,26,[33]б]). Правило, связывающее равновесную форму полиэдра ПСГ с соотношением размеров ионов кислорода и металла, уже обсуждалось в [^5,б]. Ниже обсудим два других важнейших правила.

В общем случае ПСГ в составе ВСГ могут быть связаны вершинами (однок-ратные связи), ребрами (двукратные связи) или гранями (многократные связи). Стабильность таких структур определяется правилом Полинга (цитируется по [^33б], с. 382): “наличие в координационной структуре общих ребер и особенно общих граней уменьшает устойчивость структуры. Этот эффект особенно существенен для кати-она с высокой валентностью и небольшим координационным числом“.

Данное правило обусловлено взаимным отталкиванием катионов, которые локализованы в соседствующих ПСГ. Для иллюстрации оценим интенсивность оттал-кивания одинаково заряженных частиц в типовых ситуациях. Сила отталкивания по закону Кулона пропорциональна отношению Z²/l², где Z – заряд иl - расстояние между центрами катионов. При контакте одинаковых правильных полиэдров вершинами максимальное расстояние l равно l_vv = 2R_оп, где R_оп – радиус сферы, описанной вокруг полиэдра, а минимальное расстояние при контакте гранями равно l_gg = 2R_вп, где R_вп – радиус сферы, вписанной в этот же полиэдр. Расчет l_RR при контакте полиэдров ребра-ми иллюстрируется схемой для контактирующих тетраэдров на рис. 3. Эта принци-пиальная схема применима для всех правильных полиэдров.

Сводка результатов расчета расстояний приведена в табл.1, где даны значения l_vv (контакт вершинами), l_RR – контакт ребрами и l _gg – контакт гранями, а также значения отношений l _vv/l_RR иl_vv/l_gg, которые характеризуют изменение расстояния при переходе от контакта вершинами к контакту по ребрам или граням.

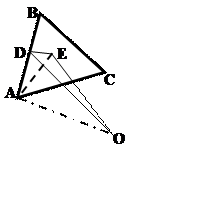Рис.3. Схема расчета расстояния между центрами правиль-ных полиэдров, контактирующих ребрами (на примере тетра-эдров): АВС - грань полиэдра (в данном случае – треугольник), ОА = R_оп, ОЕ = R_вп,OD = (1/2)l_RR = Ö[(OA)² – (AD)²] = R_опÖ[1 - (a/2R_оп)²], где а – ребро полиэдра.

Таблица 1. Изменение относительных расстояний между центрами правильных полиэдров при их контакте вершинами, ребрами и гранями, N = 4 – тетраэдр, N = 6- октаэдр, N = 8 – куб, N = 12 – икосаэдр, а – сторона полиэдра (см рис.3 на стр. 19 в [^{5, б}]).