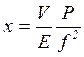
![]()
![]() , де
, де 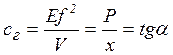 -
гідравлічна жорсткість пружини.
-
гідравлічна жорсткість пружини.
|
х Рис. 1.7. Залежність сили, прикладеної до пружини, від її переміщення |
Експериментальна характеристика відрізняється від розрахункової (рис. 1.7), тому що модуль об’ємної пружності залежить від тиску. Граничний тиск стиснення досягає 300МПа, а зміна об’єму досягає 17...18% від максимального об’єму. |
Для рідинних пружин застосовують спеціальні рідини з малим модулем об’ємного стиснення (рідини на силіконовій основі).
На характеристику пристрою впливають тиск та температура. Якщо тиск підвищується, то гідравлічна жорсткість пружини збільшується, а якщо температура підвищується, то гідравлічна жорсткість пружини зменшується.
В реальних пристроях рідину попередньо стискають. Тиск попереднього стиснення складає 30% від максимального тиску.
Задача. Діаметр циліндра (рис. 1.6) D=50 мм, діаметр плунжера d=30 мм, довжина циліндра l=250 мм. Знайдемо величину просадки амортизатора, якщо до нього прикладене навантаження 2 т (20000 Н), а модуль об’ємної пружності 1,5·109 Н/м2.
Розв’язок:
Сила рідинної пружини
![]() ,
(1.1)
,
(1.1)
де 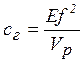 -
гідравлічна жорсткість пружини.
-
гідравлічна жорсткість пружини.
З рівняння (1.1) маємо
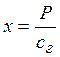 .
.
Об’єм рідини
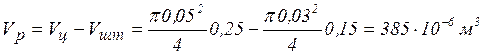 .
.
Площа плунжера
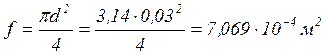 .
.
Тоді
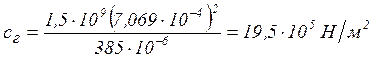 ,
,
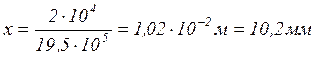 .
.
Запишемо рівняння масової витрати рідини
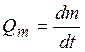 , де маса m=ρV;
, де маса m=ρV;
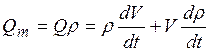 , (1.2)
, (1.2)
де ![]() -
об’ємна витрата.
-
об’ємна витрата.
З рівняння нерозривності потоку слідує, що
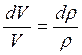 .
(1.3)
.
(1.3)
З визначення модуля об’ємної пружності слідує, що
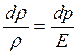 .
(1.4)
.
(1.4)
Враховуючи (1.3) і (1.4) отримуємо
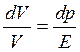 .
(1.5)
.
(1.5)
З рівняння (1.4) находимо
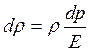
і ділимо його на dt
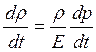 .
(1.6)
.
(1.6)
Підставимо (1.6) в рівняння (1.2) і скоротимо на ρ:
![]()
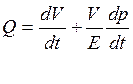 ,
(1.7)
,
(1.7)
де ![]() -
витрата рідини, обумовлена зміною робочого об’єму;
-
витрата рідини, обумовлена зміною робочого об’єму;
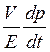 -
витрата рідини, обумовлена стисненням (динамічна витрата).
-
витрата рідини, обумовлена стисненням (динамічна витрата).
|
|
Враховуючи, що для циліндра
|
Література [2], стор. 40-45; [3], стор.56-59; [11], стор. 294-300.
З курсу гідравліки відомо, що існує два режими течії: ламінарний – шарова течія без перемішування часток і пульсації швидкості; турбулентний – режим, який супроводжується інтенсивним перемішуванням часток рідини і пульсацією швидкості. Від режиму течії залежать втрати тиску в трубопроводах і гідро пристроях.
Перехід від ламінарного до турбулентного режиму характеризується числом Рейнольдса Re.
Для трубопроводів круглого перерізу число Рейнольдса визначається так
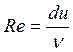 ,
(1.9)
,
(1.9)
де d – діаметр трубопроводу;
u – середня швидкість;
ν – коефіцієнт кінематичної в’язкості.
Для не круглого перерізу:
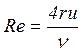 , де r –
гідравлічний радіус, який дорівнює відношенню площі до периметру:
, де r –
гідравлічний радіус, який дорівнює відношенню площі до периметру: 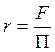 .
.
Для кільцевого трубопроводу гідравлічний радіус дорівнює
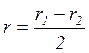 , де r1,
r2 – відповідно більший та менший радіуси кільцевого перерізу.
, де r1,
r2 – відповідно більший та менший радіуси кільцевого перерізу.
Якщо число Рейнольдса:
1) Re < Reкр, то режим течії ламінарний;
2) Re.> Reкр, то режим течії турбулентний;
де Reкр=2200-2300.
Ламінарний режим
Втрати тиску визначаються за формулами отриманими з рівняння Пуазейля
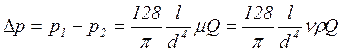 ,
(1.10)
,
(1.10)
де 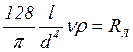 -
гідравлічний опір при ламінарному режимі.
-
гідравлічний опір при ламінарному режимі.
Тоді рівняння (1.10) можна записати
![]()
або
![]() , де
, де 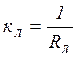 провідність
при ламінарному режимі.
провідність
при ламінарному режимі.
Якщо ввести коефіцієнт тертя 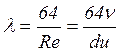 і виконати перетворення, то рівняння
(1.10) приводиться до вигляду
і виконати перетворення, то рівняння
(1.10) приводиться до вигляду
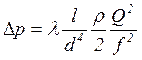 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.