Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 9

Пример расчёта энтальпии.

Пусть требуется рассчитать изменение энтальпии меди при нагреве от твёрдого состояния p = 100 атм, Т = 1200 К до Т=1400 К, p = 1 атм.

Решение:

Энтальпия – это функция состояния, поэтому её значение не зависит от пути, по которому система переходит из одного состояния в другое. Пусть процесс осуществляется так, как это показано на диаграмме рис. 2.2.

В этом случае можно записать (учтено, что температура плавления меди Т_пл = 1357 К и, следовательно, Н₁₄₀₀ = Н₁₄₀₀ (ж, р = 1 атм))

ΔН = Н₁₄₀₀(ж,p = 1 атм) – Н₁₂₀₀(тв, p = 100 атм) = Н₁₄₀₀⁰ – Н₁₂₀₀⁰ + Н₁₂₀₀⁰ – Н₁₂₀₀⁰(p = 100 атм) = (Н₁₄₀₀⁰ – Н₂₉₈⁰) – (Н₁₂₀₀⁰ – Н₂₉₈⁰) - [Н₁₂₀₀⁰ (тв, p = 100 атм) – Н₁₂₀₀⁰]

(а)                     (б) (в)

Искомая величина

ΔН = (а) – (б) – (в)

Два первых члена можно найти из справочников:

(а) = 43 806 Дж/моль;

(б) = 24 490 Дж/моль;

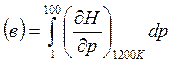                                                  (2.16)

Далее будет показано, что

(∂Н/∂p)_Т= V (1 - αT),(2.17)

здесь V – объём 1 моля меди в твёрдом состоянии, a - коэффициент термического расширения.

Так как Т – постоянна, а изменением объёма при изменении давления для твёрдого тела можно пренебречь, то, подставляя в (2.16) значение производной из (2.17) при Т=1200 К, можно получить

(в) = 80 Дж/моль, тогда               ΔН = (а) - (б) - (в) = 43 806 – 24 490 – 80 = 19 230 Дж/моль.

2.4. Теплоты реакций. Закон Гесса. Закон Кирхгоффа

Если стехиометрическое уравнение реакции записывается в виде

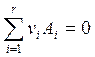                                                                 (2.18)

ν_i > 0 – для продуктов реакции; ν_i < 0 – для реагентов, то теплота реакции

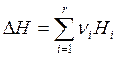,                                                            (2.19)

H_i – мольная энтальпия вещества А_i.

Если ΔН > 0, то теплота поглощается системой, и говорят, что реакция эндотермическая, если ΔН < 0, то система выделяет теплоту, и говорят, что реакция экзотермическая.

В частности, если имеем

x A + y B = A_x B_y, обозначим А = А₁, В = А₂, А_хВ_y  = А₃, тогда ν₁ = -x, ν₂ = -y, .

Следовательно, ΔН = Н(А_xВ_y) – xH(A) – yH(B)

Если вещество в стандартном состоянии, то

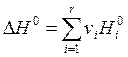.                                                         (2.20)

ΔН (или ΔН⁰) – это теплота реакции, которая выделяется в результате реакции при полном превращении ν_i молей реагента А_i (где i = 1, ….k) в ν_i продуктов А_i (где i = k + 1, …r), т.е.

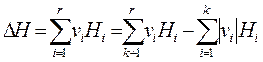                                           (2.21)

(Необходимо помнить ν_i> 0 – для продуктов реакции; ν_i < 0 – для исходных продуктов).

Соотношение (2.19) или (2.21) выражают закон Гесса, в соответствии с которым (1840 г.) тепловой эффект реакции не зависит от пути процесса (набора промежуточных стадий), а определяется только начальным и конечным состоянием системы (это следствие того, что Н – функция состояния).

На практике в системе, содержащей n_i молей разных веществ А_i (i = 1, …r), часто оказывается, что реакция не протекает полностью.

Если ввести в рассмотрение величину ξ, называемую степенью полноты реакции (или химической переменной, или координатой реакции), с помощью соотношения

(n₁ – n₁₀)/ν₁ = (n₂ – n₂₀)/ν₂ = …………= (n_r – n_r0)/ν_r = ξ

или

dn₁/ν₁ = dn₂/ν₂ = ……… = dn_r/ν_r  = dξ ,(2.22)

здесь индекс «0» означает начальное состояние системы, то можно записать универсальное соотношение, которое будет справедливо как в случае полного протекания реакции, так и неполного.

Действительно, энтальпия системы, содержащей n_i молей вещества (компонента) А_i (i = 1…r),

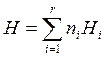.                                                             (2.23)

При p = const, T = const изменение энтальпии системы ΔН_s в результате реакции

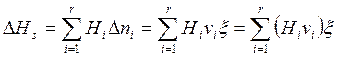                            (2.24)

Или, так как в соответствии с (2.22) dn_i = ν_i dξ

dH_s = ΔH dξ                                                                (2.25)

Т.е. увеличение энтальпии системы – это произведение теплоты протекающей реакции ΔН на степень полноты её протекания (координаты реакции).

Необходимо отметить, что, если:

dξ > 0 – имеет место прямая реакция (число молей продуктов возрастает, реагентов уменьшается);