Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 42

,                                                                   (12.1)

где К_Г, как и в случае растворения газа в конденсированной фазе называют константой Генри.

Уравнение (12.1) описывает уравнение изотермы адсорбции Генри. В принятой модели концентрация поверхностных молекул пропорциональна давлению в системе.

Зачастую вместо понятия «поверхностная концентрация» используют понятие «степень заполнения». Дело в том, что поверхность не обладает бесконечной емкостью. Если адсорбированные молекулы будут плотнейшим образом упакованы на поверхности, то это означает максимальное заполнение поверхности. Соответствующая поверхностная концентрация отвечает максимально возможной концентрации при заполнении поверхности в виде монослоя - Г_∞. Под степенью заполнения понимают величину

.                                                        (12.2)

Следовательно, уравнение (12.1) можно написать в следующем виде:

                                                  (12.3)

Линейный закон, определяемый выражением (12.3), выполняется при небольших степенях заполнения.

12.2. Изотерма адсорбции Ленгмюра

Учет степени заполнения приводит к более реальной картине заполнения монослоя. В этом случае равновесие следует записывать так:

М + свободная поверхность = М_п.

Если полное число мест на поверхности N_П, то число свободных мест равно (1 - θ) N_П (θ - степень заполнения поверхности), а занятых θN_П. Если при этом полагать, что все центры адсорбции идентичны и нет бокового («латерального») взаимодействия между адсорбированными молекулами, то константа равновесия адсорбции К в этом случае определит следующее равновесие:

, где f – летучесть; γ_П – коэффициент активности поверхностных молекул в газовой фазе; θ – степень заполнения поверхности.

Если принять, что f ≈ p, то

.

Если предположить, что  то

,                                                        (12.4)

или

.                                                        (12.5)

Уравнение (12.5) представляет собой уравнение изотермы Ленгмюра. Зависимость θ от р для этой изотермы изображена на рис. 12.1.

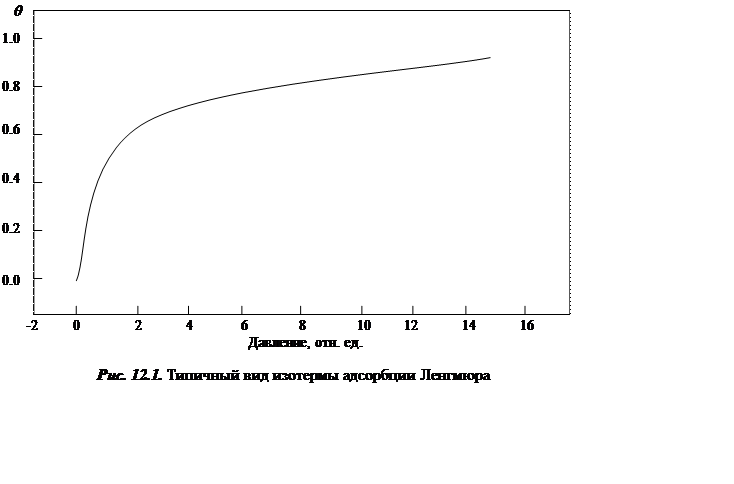
Если р мало (К р << 1), уравнение Ленгмюра переходит в уравнение Генри:

.

Для анализа экспериментальных данных по адсорбции уравнение изотермы Ленгмюра удобно представить в следующем виде:

.

Уравнение адсорбции Ленгмюра легко следует из простых кинетических соображений. В равновесии число молекул, улетающих с поверхности в единицу времени, равно числу молекул, попадающих на поверхность за это же время. Число молекул, улетающих в единицу времени с поверхности N_дес, равно

, где к_дес - некоторый коэффициент, характеризующий скорость десорбции. Число молекул, адсорбирующихся на поверхности (N_адс), пропорционально давлению и величине незанятой поверхности:

, где к_адс - коэффициент, характеризующий скорость адсорбции. Отсюда, приравнивая N_дес = N_адс, находим

.

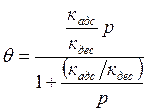Сравнение этого выражения с выражением (12.5) показывает, что

.

12.3. Изотерма адсорбции БЭТ

Если адсорбирующийся газ находится при температуре ниже критической, то нередко наблюдают полимолекулярную адсорбцию, особенно при давлении газа вблизи давления насыщенных паров его конденсированной фазы. Полимолекулярную адсорбцию в простейшем случае можно описать следующей системой химических уравнений:

М + (свободная поверхность) → М₁

М + М₁ → М₂

....

М + М_i-1 → М_i, где М_i – кластер ,состоящий из i-молекул. Кластеры различного строения показаны на рис. 12.2.

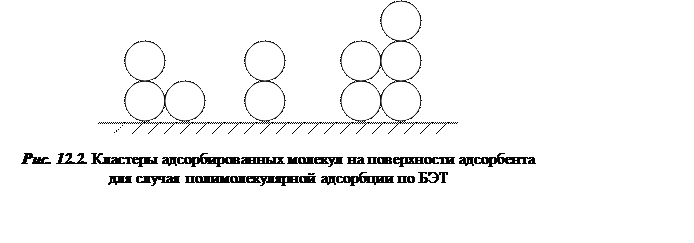
Обратимся к анализу уравнений, описывающих адсорбцию данного типа. Для простоты все коэффициенты активности положим равными единице. Степень заполнения поверхности кластерами из i молекул обозначим через θ_i, константу равновесия образования i-го кластера обозначим через К_i. Долю свободной поверхности обозначим через θ₀. Тогда

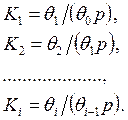                                                             (12.6)

Константы равновесия К_i, вообще говоря, не одинаковы. Однако для простоты расчетов можно полагать, что все константы равновесия с равны друг другу: