Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 39

Могут быть две различные ситуации, показанные на рис. 10.4 (а, б).

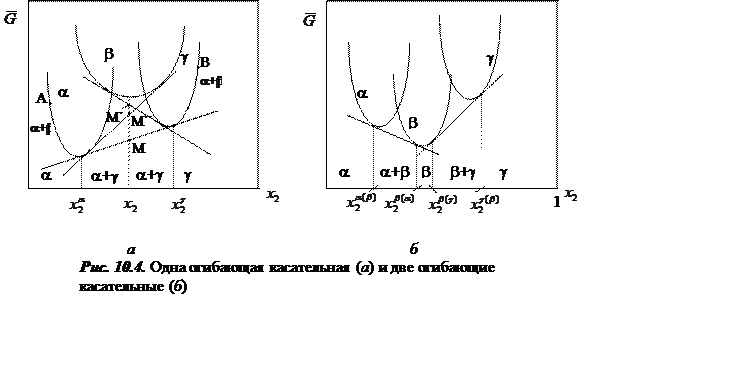
Случай «а». Проведены касательные к каждой паре кривых  В данном случае (рис. 10.4, а) кривая  не пересекает касательную  следовательно, любая точка на касательных  и  (точки M´ и М´´) будет находиться выше точки М. Следовательно, состояния, в которых будет присутствовать фаза b, будуть метастабильными (устойчивыми только к малым колебаниям) или вообще неустойчивыми

Случай «б». Кривая (см рис.10.4) пересекает касательную . В этом случае в зависимости от концентрации  можно иметь состояния, в которых присутствуют только a, a + b, b, b + g и g.

Приведенные построения справедливы для систем с любым числом фаз. При этом для определения энергии Гиббса системы в ее наиболее стабильном равновесном состоянии можно использовать простое правило: молярная Энергия Гиббса системы в ее наиболее стабильном равновесном состоянии изменяется по кривой, совпадающей с туго натянутой струной, огибающей кривые , закрепленной в точках А и В на крайних левых и правых кривых .

10.4 Две фазы в бинарной системе, представляющие идеальные растворы

Анализ равновесий тв – ж, тв₁ – тв₂, ж – газ идентичен.

Рассмотрим систему тв – ж.

Пусть характерные зависимости для этой системы соответствуют рис. 10.5.

На рис.10.5 температура от «а» к «д» уменьшается. При высоких Т  при всех  - жидкое состояние более устойчиво. С понижением температуры , при  (рис. 10.5, б). Дальнейшее снижение температуры приводит к ситуации, когда кривые  и  пересекаются (рис. 10.5, в). В этом случае можно провести общую касательную, которая даст точки  и , определяющие равенство химических потенциалов веществ 1 и 2 в твердом и жидком растворах.

При  - жидкость,  - тв + ж,  - тверд.

Дальнейшее снижение температуры (рис. 10.5, г)  только при .

При более низких температурах вся кривая  оказываетсят над  - твердое состояние более устойчиво при всех .

Фазовая диаграмма, отражающая зависимость состава от температуры, для рассматриваемой системы представлена на рис.10.5, е. Здесь 1 - линия ликвидуса, 2-линия солидуса.

Для идеальных растворов (растворы, для которых а_i = х_i ) линии ликвидуса и солидуса могут быть определены аналитически.

Согласно (10.8) в случае равновесия . Положив  (влияние давления для жидких и твердых сред невелико; * - состояние сравнения, 0 - стандартное состояние), можно записать, учитывая, что

.                                    (10.12)

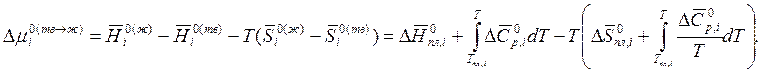 (10.16) (10.13)

Опустим для простоты записи черту над символами, обозначающими молярные свойства.

Будем рассматривать случай, когда . В этом случае

,                        (10.14)

где  и  - изменения энтальпии и энтропии в результате фазового перехода (при температуре плавления).

При ,

,                                                         (10.15)

откуда

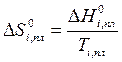.                                                           (10.16)

Подставляя (10.16) в (10.14), получаем

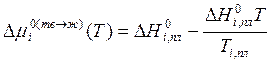.                                           (10.17)

Учитывая (10.17), из (10.12) для i = 1 получим

.                                  (10.18)

Так как растворы идеальны  ( - мольная доля компонента 1), то с учетом (10.18) получим

.                                     (10.19)

Соответственно, для , аналогично

                                     (10.20)

Так как  (по определению 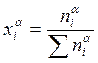, ), то, складывая (10.19) и (10.20), получаем уравнение линии солидуса:

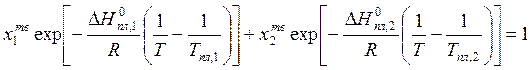.               (10.21)

Выражая из (10.19), (10.20) и  и учитывая, что , получаем уравнение линии ликвидуса

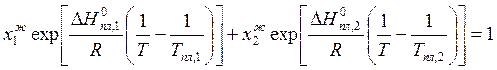.                      (10.22)

Системы, которые не сильно отклоняются от идеальных, имеют качественно аналогичные зависимости.

Интересно оценить интервал  между линиями ликвидуса и солидиуса в сечении 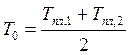. Если предположить, что  (это часто хорошо выполняется), то, учитывая (10.16), можно получить, что

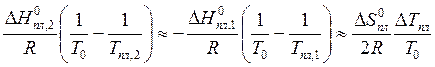,                                   (10.23)

где .

Теперь из (10.20)

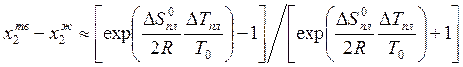.                             (10.24)

Имея ввиду, что 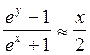 (из разложения в ряд Тейлора, 1-е приближение), можно записать