Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 8

dw = + p dV ,(2.2)

где р – внешнее давление; dV – изменение объёма (dV > 0 – при расширении, dV < 0 – при сжатии). Работа не является функцией состояния.

Теплота определяется как изменение внутренней энергии при отсутствии работы. Теплота не является функцией состояния.

Внутренняя энергия системы. Если это газ, в котором изменяться может лишь кинетическая энергия молекул, то состояние газа можно описать, задав внутреннюю энергию в виде

U = U₀ +U_молек,            (2.3)

где U_молек – кинетическая энергия молекул газа; U₀ – прочие виды энергии (энергия химических связей, внутриатомного взаимодействия – эту часть внутренней энергии можно определить на основе уравнения Эйнштейна U = mc² и т.д.).

Очевидно, во всех процессах сжатия, расширения, нагрева газов до температуры ниже температуры ионизации U₀ изменяться не будет, поэтому

dU ≡ dU_молек.                                                               (2.4)

Следовательно, чтобы описать dU, необходимо найти способ, как описать изменение энергии молекул. Для идеального газа U_молек.однозначно связана с температурой.

При рассмотрении химических превращений, явлений на поверхности и некоторых других процессов требуется более детальное рассмотрение U с учётом взаимодействия атомов и молекул на поверхности и внутри молекул.

2.2. Теплоёмкость, энтальпия

Определение теплоёмкости (С):

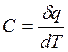.                                                                     (2.5)

С – не функция состояния, С – зависит от пути процесса (С_V, C_p и т.д.)

Если работа, совершаемая системой, связана только с преодолением внешнего давления при её расширении [см. (2.2)]

dw = + p dV

тогда на основе (2.1)

dU = δq – pdV                                                                        (2.6)

При постоянном объёме (изохорический процесс: dV = 0, или V = const)

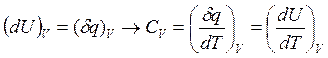                              (2.7)

Как уже говорилось, нижний индекс, отражающий термодинамический параметр, означает, что процесс протекает при постоянном значении этого параметра.

При постоянном давлении (изобарический процесс р=const) удобно ввести функцию состояния, называемую энтальпией.

H ≡ U+pV                                                                  (2.8)

Полный дифференциал

,                                                          (2.9)

или

, если р = const →                            (2.10)

.                                                (2.11)

Из (2.6), (2.11)

δq = dU + pdV  →                                                     (2.12)

                                                               (2.13)

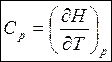                                                              (2.14)

С использованием второго закона термодинамики можно получить

С_p – С_V = α² VT/β, где

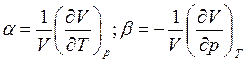                                               (2.15)

α, β – коэффициенты теплового расширения и изотермического сжатия.

Для некоторых систем (например, идеальный газ) теплоёмкости можно рассчитать теоретически, для большинства случаев используются экспериментальные данные.

Энтальпия (и другие функции состояния) обычно определяется относительно некоторого стандартного состояния. Например, относительно  - энтальпии при p = 1 атм и Т = 298К, как это показано на рис. 2.1.

2.3. Стандартные состояния (р = 1 атм, наиболее устойчивая структура)

В химической термодинамике рассматриваются процессы, характеризующиеся атомарной структурой системы, т.е. на уровне взаимодействия атомов и молекул. Процессы типа ядерных, проходящие с заметным изменением массы, не рассматриваются. При этом в расчётах всегда приходится иметь дело только с относительными изменениями функций состояния реагирующих веществ.

В этих условиях удобно, особенно при составлении термодинамических таблиц, иметь дело со стандартными состояниями.

Обычно за стандартное состояние вещества принимают его состояние при давлении 1 атм со структурой, наиболее стабильной для данного вещества при температуре его исследования (например, идеальный газ для газов, О.Ц.К. структура Fe_α для железа). Свойство системы в стандартном состоянии (стандартное свойство) обычно обозначается правым нулевым индексом. Например, стандартная энтальпия и теплоёмкость  обозначаются Н⁰ и С_p⁰ соответственно. Стандартные энтальпии при различных температурах обычно табулируются в виде Н_Т⁰ - Н₂₉₈⁰.