Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 43

, где р⁰ - давление насыщенных паров. Это предположение означает, что кластер, в состав которого входит больше двух молекул, в отношении адсорбции и десорбции подобен чистой жидкости. Конечно, это очень грубое приближение. Тем не менее, оно позволяет получить простые аналитические выражения для описания процесса полислойной адсорбции. В этом случае уравнения (12.6) принимают вид:

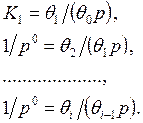                                              (12.7)

Выражая величины θ_i через θ₀, получаем

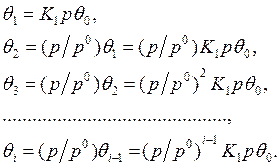                            (12.8)

Используя условия сохранения числа мест адсорбции на поверхности

получаем

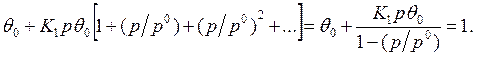
Отсюда

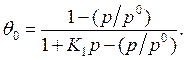                                                 (12.9)

Количество молекул на поверхности (N_адс) с учетом полимолекулярной адсорбции равно

                                      (12.10)

В этой формуле N_П - максимальное заполнение монослоя. Коэффициент «i» перед θ_i в сумме в выражении (12.10) возникает из-за присутствия i молекул в i-м кластере. При этом сумма в (12. 10) равна

Величина  представляет собой производную ряда  по . И следовательно, так как сумма геометрической прогрессии

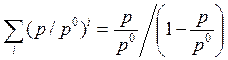, то

.

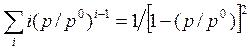Итак,

                                (12.11)

Подставляя в формулу (12.11) выражение для θ₀ из формулы (12.10), находим

Величину К₁р⁰ обычно обозначают через с. Как правило, с >> 1. Тогда:

                           (12.12)

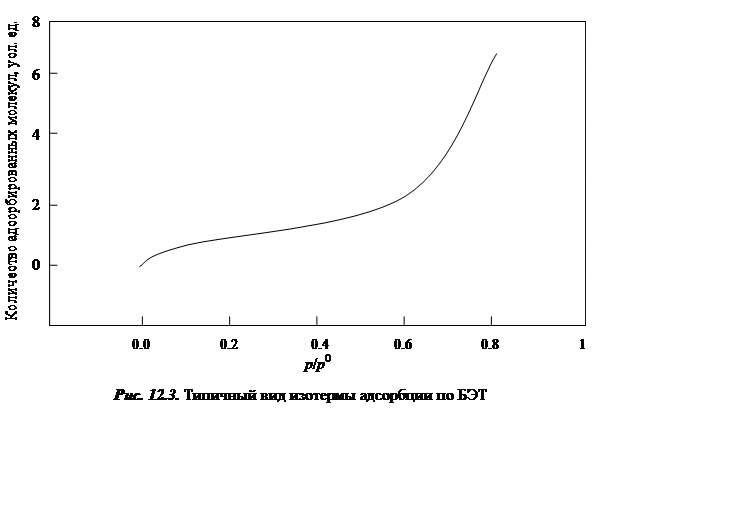
Уравнение (12.12) называется уравнением Брунауэра, Эммета и Теллера (БЭТ). Пример изотермы адсорбции, рассчитанной по уравнению (12.12), приведен на рис. 15.3.

Из выражения (12.12) легко получить формулу, удобную для построения экспериментальных данных в виде линейных анаморфоз:

.

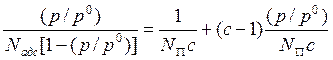Обработка экспериментальных данных по величине адсорбции в зависимости от давления в координатах 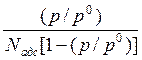 -  позволяет получить значения для N_П и с. Величина N_П характеризует число мест адсорбции на поверхности.

Уравнения БЭТ используют при определении величин поверхности, так как, зная N_П, массу образца m и площадь, занимаемую одной молекулой S₁, можно определить поверхность единицы массы пористого образца, используя соотношение

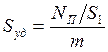
12.4. Уравнение адсорбции Гиббса

Адсорбция на поверхности влияет на величину коэффициента поверхностного натяжения. Поэтому, зная зависимость коэффициента поверхностного натяжения от концентрации, также можно судить о величине адсорбции. Эта связь устанавливается с помощью уравнения адсорбции Гиббса. Его можно получить с помощью аналога уравнения Гиббса - Дюгема в применении к поверхностным процессам.

Уравнение Гиббса - Дюгема ранее (см. гл. 5.2) было выведено исходя из однородности энергии Гиббса для системы, содержащей несколько компонентов. В случае нескольких фаз необходимо учесть поверхностную энергию. В этом случае внутренняя энергия U^S, будет иметь вид

.                                        (12.13)

Здесь и далее индекс «s» указывает на величину, определяемую с учетом взаимодействий на поверхности. S_a – площадь поверхности.

Для получения аналога уравнения Гиббса-Дюгема достаточно рассмотреть полный дифференциал уравнения (12.13):

                 (12.14)

Учитывая поверхностную энергию и пренебрегая изменением объема твердого тела, соотношение (5.5) для рассматриваемого случая можно записать в виде

                                            (12.15)

Приравнивая правые части (12.14) и (12.15), находим аналог уравнения Гиббса-Дюгема

                                                 (12.16)

Обычно процессы исследуют при Т = const. Тогда последнее уравнение переходит в

                                                  (12.17)

или

,                                                       (12.18)

где

                                                       (12.19)

представляет собой избыток i-го вещества в поверхностном слое (поверхностную концентрацию адсорбированного вещества по Гиббсу).

В случае двухкомпонентной системы

.                                    (12.20)

Если Г₁ характеризует растворитель, а Г₂ - растворенное вещество, то, выбирая границу раздела так, чтобы Г₁ = 0, получаем

.