Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 13

Получается, если в (3.36) положить .

4)        Если положить в (3.34) , то 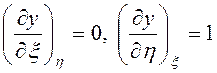 и получается

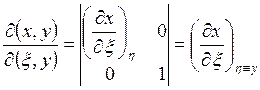. Аналогично  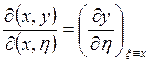                         (3.38)

Определение (3.34) и основные свойства якобианов (3.35)-(3.38) будут полезны в дальнейшем при определении и вычислении различных функций состояния и термодинамических коэффициентов.

Политропические процессы

Рассмотрим термодинамический процесс с произвольной, но постоянной теплоемкостью – политропический процесс. Имеем [см (2.5), (2.7)]

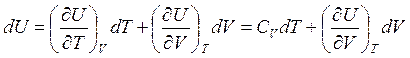 , .                    (3.39)

Вычислим 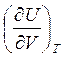, учитывая, что 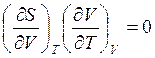, т.к.

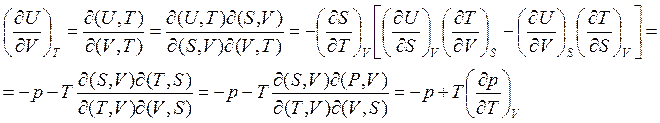   (3.40)

При выводе (3.40) были использованы выражения, следующие из (3.14):

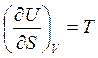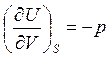 ,                                                    (3.41)

Подставив в (3.39) выражение для первого закона термодинамики (2.1) и формулу (3.40), получим

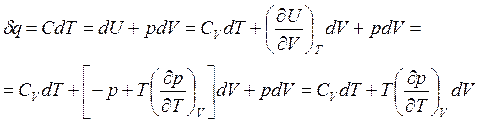                        (3.42)

Следовательно,

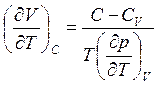                                                                (3.43)

Если известно уравнение состояния p = p(T,V), то уравнение (3.43) может быть проинтегрировано, что приводит к уравнению политропы T = T(V). Используя уравнение состояния, последнюю зависимость можно представить в виде p = p(V), либо T = T(p).

Проделаем процедуру интегрирования для совершенного газа (pV = RT, C_V = const). Уравнение (3.43) принимает вид:

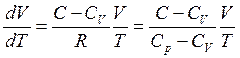 или 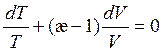,                  (3.44)

где постоянная величина æ называется показателем политропы

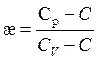.                                                                           (3.45)

Интегрируя (3.44), получаем уравнение политропы TV^æ-1 = const или (с учетом уравнения состояния) pV^æ = const или T^-æ p^æ-1 = const.

Частные случаи политропических процессов

Энтропия и энтальпия совершенного газа

Определим энтропию и энтальпию как функцию термодинамических параметров. Из уравнения (3.14) для дифференциала внутренней энергии выражается дифференциал энтропии

                                                      (3.46)

С учетом уравнения состояния идеального газа (1.5) и выражения  для внутренней энергии совершенного (C_V = const) газа (3.46) переходит в

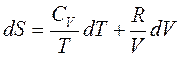                                                (3.47)

Интегрируя (3.47), получаем

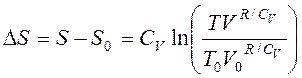                        (3.48)

Из (3.48) можно поучить выражение для внутренней энергии совершенного газа как функции собственных переменных (S, V):

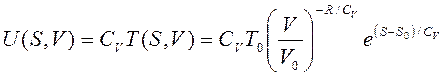                   (3.49)

Используя уравнение состояния, можно выразить изменение энтропии (3.48) через другие пары параметров:

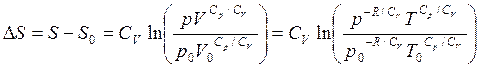                        (3.50)

Энтальпия идеального газа

                       (3.51)

Энтальпия совершенного газа

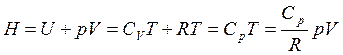                            (3.52)

Изобарический процесс , , , – закон Гей-Люссака. В этом случае из (3.50) процесс удобно представить в виде (3.54):

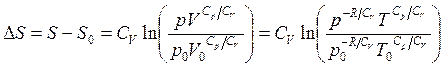                   (3.53)

                                                      (3.54)

Изотермический процесс , , ,  - закон Бойля -Мариотта.

Адиабатический процесс ,  (показатель адиабаты), , ,  - закон Пуассона.

Изохорический процесс , , ,  - закон Шарля (самый древний, выведен в 17 веке). Для (T, S)-координат из (3.50) процесс представляется в виде (3.56):

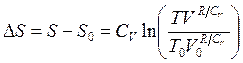                                               (3.55)

                                                       (3.56)

Все эти процессы можно представить на рабочей (рис. 3.2) и тепловой (рис. 3.3) диаграммах.

Из определения показателя политропы (3.45) следует:

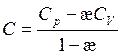                                                            (3.57)

Из (3.57) следует, что положительные теплоемкости C > 0 имеют место при  -¥ < æ < 1  и  g < æ < ¥, а интервал  1 < æ < g  соответствует отрицательным теплоемкостям.

3.4. Основные соотношения термодинамики закрытой системы (работа связана только с преодолением внешнего давления: dw = pdV)

Мы видели, что использование той или иной термодинамической функции при осуществлении того или иного процесса позволяет получить наиболее простые соотношения, описывающие изменение системы. Такого рода функции называются характеристическими. Более точно: