Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 28

7.8. Зарождение и рост новой фазы

7.8.1. Движущая сила при переходе системы в состояние равновесия

Пусть

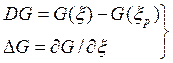 - обозначения.                                   (7.20)

Величина ¶G/¶x называется движущей силой процесса установления равновесия (G – энергия Гиббса, x - параметр возмущения термодинамической системы, ξ_р – значение параметра в равновесном состоянии системы).

Если отклонение от равновесия невелико, то G(x) можно разложить в ряд Тейлора в окрестности точки x_р с учётом, что в точке равновесия :

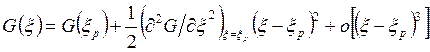.                                    (7.21)

Отсюда (учтём, что G(x_р) = const, )

.                                        (7.22)

Выражая из (7.21) DG = G(x) – G(x_р),можно получить

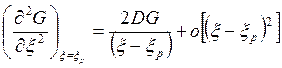.                                         (7.23)

Подставляя (7.23) в (7.22), получаем

.                                            (7.24)

Это общее соотношение для движущей силы процесса установления равновесия.

7.8.2. Минимальный размер зародыша новой фазы

Чтобы при заданной движущей силе процесс образования новой фазы имел место, необходим определённый размер зародыша.

В отсутствии новой фазы зародыши этой фазы образуются за счёт атомных (молекулярных) флуктуаций в виде включений очень малых размеров.

Существует некий критический размер зародыша, ниже которого новая фаза при заданной движущей силе не образуется, а выше - образуется.

При образовании новой фазы затрачивается работа на создание новой поверхности

,                                                         (7.25)

где s - поверхностное натяжение между фазами зародыша β и матрицы a, dА – приращение поверхности.

Можно установить, что при образовании зародыша

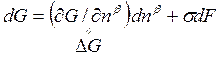.                                          (7.26)

Если зародыш – сфера радиусом r, то

,                                                        (7.27)

,                                                                    (7.28)

где n^β – число молей вещества в фазе β,  - молярный объем вещества в фазе β

Следовательно,

,                               (7.29)

DG = ¶G/¶n^b -химическая движущая сила, определяемая соотношением (7.24).

Если , то , так как .

Величина DG < 0, а s > 0, поэтому функция (7.29) имеет максимум G^max(r) = G(r_c) (см. рис. 7.9.)

При r < r_c – зародыши нестабильны (G - увеличивается с увеличением r).

При r > r_c – зародыши стабильны и растут. r_c находится из (7.29) на основании условия

,                                                          (7.30)

.                                                            (7.31)

Необходимая энергия для достижения r_c (энергия активации) определяется путём подстановки (7.31) в (7.29) ®

.                                          (7.32)

Таким образом, чем выше s, тем больше r_c[см. (7.31)]; чем выше (¶G/¶x), тем меньше r_c.

8. Равновесия фаз в многокомпонентных системах

8.1. Общий метод анализа равновесия фаз

1.  Производится уточнение, по каким компонентам и фазам систему можно считать не взаимодействующей (скорость изменения этих компонентов очень мала или равна нулю по сравнению со скоростью изменения остальных).

2.  Принимается минимальный размер системы, в рамках которой происходит интересуемый процесс и которую можно считать закрытой гетерогенной системой.

3.  В рамках закрытой многокомпонентной гетерогенной системы, состоящей из α, β, … θ фаз, выделяются открытые многокомпонентные системы (которые могут быть гетерогенными), взаимодействующие между собой в рамках общей закрытой системы.

4.  Далее используются общие критерии равновесия для закрытой системы и частные условия для каждой из однокомпонентных открытых систем.

8.2. Условия равновесия закрытой многофазной системы

Пусть имеем закрытую гетерогенную систему, состоящую из гомогенных открытых систем (фаз). α, β, … θ - фазы гетерогенной системы, n₁ⁿ, n₂ⁿ, … n_mⁿ - содержание компонентов 1 ... m в фазе n.

Критерий равновесия для этой закрытой системы в соответствии с (3.16):

.

Пусть объём и энтропия всей системы неизменны (S, V = const), тогда условие равновесия можно записать в виде

.                                                               (8.1)