Другие предметы \ Химическая термодинамика

Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 14

Характеристической называется функция состояния независимых параметров, характеризующаяся тем, что посредством этой функции и ее производных по этим параметрам могут быть выражены все термодинамические свойства системы.

При определённом наборе переменных, характерных для каждой термодинамической функции, каждая из термодинамических функций (функций, являющихся полным дифференциалом) может рассматриваться как характеристическая.

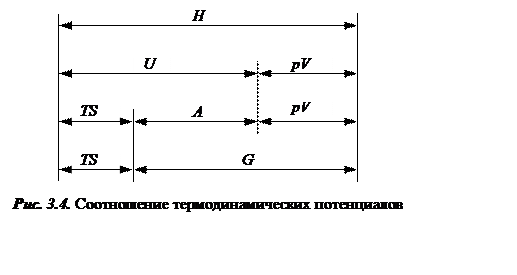
Соотношения между термодинамическими функциями (потенциалами)

Наглядно определения термодинамических потенциалов и связь между ними проиллюстрированы на рис.3.4 и в таблице 3.1.

Используя свойства полных дифференциалов, можно получить уравнение Максвелла [см. уравнение (1.11)].

Основные уравнения термодинамики закрытых систем представим в виде следующей таблицы (табл. 3.1).

Таблица 3.1

Постоянные процессы

Характеристическая функция

Дифференциал

Критерий равновесия

δZ = (δU –

- TdS +

+ pdV) ≥ 0
Соотношения Максвелла

Изохорно-изоэнергетический процесс

dS = δqобр/T

(dS)U,V ≤ 0

-

U, V

S

Изохорно-изоэнтропийный

dU = TdS - pdV

(δU)S, V ≥ 0

S, V

U

Изобарно-изоэнтропийный

dH = TdS + Vdp

(δH)S, p ≥ 0

 

S, р

H ≡ U + pV

Изохорно-изотермический

dA = -SdT - рdV

(δA)T,V ≥ 0

 

T, V

A = U – TS

Изобарно-изотермический

dG = - SdT + Vdp

(δG)T, p ≥ 0

 

T, р

G ≡ U + pV – TS

Манипулируя соотношениями для dU, dH, dA, dG [выражения (3.14), (3.20), (3.27), (3.32)] и другими формулами, содержащимися в табл. 3.1, можно получить много других полезных соотношений, связывающих термодинамические функции и свойства системы.

Например, разделив (3.20) на dT, получим

(∂H/∂T)p = T(∂S/∂T)p(3.58)

или

(∂S/∂T)p = Cp/T ,             (3.59)

откуда изменение энтропии при изобарическом процессе:

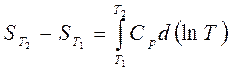.                                                 (3.60)

Получить самостоятельно:

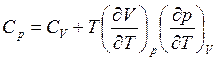
Примеры следствий из соотношений Максвелла

По определению термический коэффициент расширения 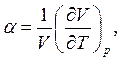 т.е. 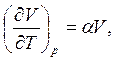 следовательно, из соотношения Максвелла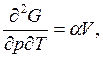

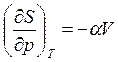                                                            (3.61)

Тогда, используя (3.20),

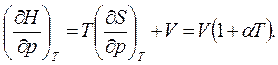                                        (3.62)

Задание:

1) показать, что для идеального газа (это означает pV = nRT ) энергия зависит только от температуры (т.е. (∂U/∂V)T = (∂U/∂р)T = 0);

2) найти связь между Сp и СV для идеального газа (Cp - CV = α2VT/β – в общем случае).

4.ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ

4.1. Формулировка Нернста (1906)

При Т = 0 в обратимых реакциях для идеальных кристаллов ΔS = 0 – Нерст, 1906.

4.2. Формулировка Льюиса (1923)

Если принять, что S = 0 при Т = 0 для любого элемента в идеальном кристаллическом состоянии, то каждое вещество, состоящее из этих элементов, имеет конечное положительное значение энтропии, однако при Т = 0 энтропия может обратиться в нуль и в случае идеального кристаллического вещества обращается в нуль.

4.3. Формулировка Гугенгейма (1949)

Температура, равная абсолютному нулю, не достижима.

Все эти формулировки эквивалентны.

Смысл третьего закона термодинамики с точки зрения статистической термодинамики состоит в том, что при Т = 0 состояние системы, находящейся в истинном термодинамическом равновесии, отвечает самому низкому квантовому состоянию (истинное термодинамическое состояние – состояние идеально упорядоченного вещества, например, идеальные кристаллы).

Следствия третьего закона

Изменение энтропии в изобарическом и изохорическом процессах за счёт изменения Т:

Скачать файл