Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 23

тогда, решая систему уравнений (6.54), (6.56), (6.58) относительно ,  и подставляя в (6.52), можно получить:

                                            (6.59)

Итак, для того чтобы определить равновесные концентрации веществ, необходимо:

¨  решить вопрос о том, какие индивидуальные вещества надо рассматривать при решении задачи (пусть число этих веществ будет m) и какие и сколько химических элементов входят в состав рассматриваемой системы (пусть их будет l);

¨  рассмотреть r уравнений диссоциации (r = m - l) и r соответствующих уравнений, выражающих закон действия масс для каждой реакции (или r других независимых уравнений реакций)

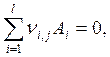         j = 1 … r                                                (6.60)

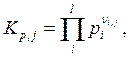          j = 1 … r;                                            (6.61)

¨  в систему уравнений термодинамического равновесия для идеальной газовой смеси необходимо включить также закон Дальтона:

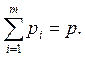                                                                      (6.62)

Для замыкания системы уравнений необходимо записать ещё (n - 1) уравнений материальных балансов (неизменность отношения числа атомов разного типа в смеси в исходном и равновесном состояниях):

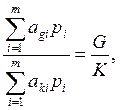                                                                        (6.63)

где а_gi и a_ki – количество атомов вида g и k соответственно в молекуле i-того вещества; G и К – суммарные количества атомов вида g и k в исходных реагентах (G/K - отношение чисел атомов вида g и k в исходных продуктах).

Уравнения материального баланса (6.63) записаны с учётом того, что 1 моль любого вещества содержит одинаковое количество молекул, равное числу Авогадро (А), а величина р_i /р - доля молекул вида i от общего числа молекул в реакционной смеси.

Таким образом, имеется:

▸  m - l уравнений (6.61);

▸  1 уравнение (6.62);

▸  l - 1 уравнений (6.63);

▸  Всего m – l + 1 + l – 1 = m уравнений для определения m значений парциальных давлений, т.е. задача может быть решена.

Часто удобно оперировать не в терминах парциальных давлений, а в мольных долях (x_i). Для того чтобы получить соответствующую систему уравнений, необходимо в (6.61), (6.62), (6.63) сделать подстановку р_i = х_i р, после чего можно найти:

▸  закон действия масс

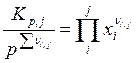         j = 1 … r                                 (6.64)

▸  закон Дальтона

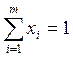;                                                                    (6.65)

▸  уравнение баланса элементов в реакционной смеси

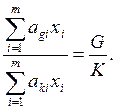                                                             (6.66)

В случае, если требуется перейти к числам молей соответствующих компонентов n_i = х_in (n-общее число молей реакционной среды), то необходимо добавить еще одно уравнение, выражающее равенство числа атомов каждого вида до реакции и после реакции и позволяющее определить n:

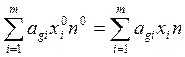.                                                          (6.67)

Пример: диссоциация водорода

H₂ Û 2 H.                                                       (6.68)

Введем обозначения: нижний индекс i-номер компонента;

H₂ – i = 1,       H – i = 2.                                             (6.69)

Уравнения:

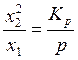,                                                       (6.70)

,                                                      (6.71)

.                                                   (6.72)

Изменение объема

b=n/n⁰=2x₁/(2x₁+x₂).                                                  (6.73)

В данном случае имеется три уравнения для определения трех неизвестных х₁, х₂, b.

7. Равновесия ФАЗ В ОДНОКОМПОНЕНТНЫХ СИСТЕМАХ (ЗАКРЫТЫЕ СИСТЕМЫ)

Пусть имеем чистое однокомпонентное вещество (например, железо или СО₂ или любое другое). Известно, что вещество может быть твёрдым, жидким или газообразным; в твёрдом состоянии вещество может находиться в различных кристаллических состояниях. Все эти различные состояния называются фазами. Область существования каждой фазы вполне определённая (в определённом диапазоне температур и давлений).

7.1. Фазовые переходы первого и второгорода