- Уравнение Менделеева-Клапейрона для идеального газа (газ, состоящий из частиц, между которыми силы притяжения и отталкивания отсутствуют, размер частиц бесконечно мал)
рV = RT, (1.5)
где R – молярная газовая постоянная (R = 8,31451 Дж/(моль·К)); V – объём одного моля газа (молярный объем).
- Уравнение Ван-дер-Ваальса для неидеального газа.
(p + a/V2) (V - b) = RT, (1.6)
где а, b – коэффициенты, учитывающие взаимодействие между молекулами и собственный объём молекул.
Существуют другие уравнения состояния неидеального газа.
Если система представляет собой смесь различных компонентов, то необходимо в описание системы вводить дополнительные параметры, характеризующие её состав. Число таких дополнительных параметров зависит как от числа компонентов, так и от числа фаз.
Функция состояния – функция, значение которой определяется только параметрами системы и которая не зависит от пути перехода системы в то или иное состояние. Например, давление идеального газа – однозначная функция объема и температуры. Величина работы, например, зависит от пути перехода системы в конечное состояние, и поэтому не может рассматриваться как функция состояния.
При расчете изменений любых функций состояния ΔF в любых процессах или реакциях принято следующее правило знаков. Из величины F для конечного состояния F(кон) вычитают величину F для начального состояния F(нач):
ΔF = F (кон) – F (нач)(1.7)
Для решения вопроса о том, является ли рассматриваемая величина функцией состояния или нет, существуют простые математические критерии. Напомним эти критерии на примере некоторой величины A(x,y), зависящей от двух переменных x и y. При изменении x и y ее приращение можно записать в следующем виде:
δA (x, y) = L (x, y) dx + M (x, y) dy, (1.8)
где L(x, y) и M(x, y) – некоторые функции. Это выражение может быть полным дифференциалом, но может и не быть им. Если выражение δA(x, y) представляет собой полный дифференциал, то исследуемая величина представляет функцию состояния.
Дифференциал (или, говорят, полный дифференциал) функции двух переменных А(x, y) определяется как линейная часть приращения ее аргументов и записывается как
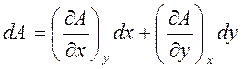(1.9)
Здесь и далее нижний индекс означает, что производная берется при постоянном значении переменной, имеющей то же обозначение, что и индекс.
Например, выражение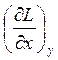 
означает, что производная вычисляется при
постоянном значении переменной y.
Перекрестные частные производные (если они непрерывны) тождественно равны
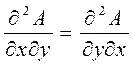(1.10)
То есть, если dA =L(x, y)dx + M(x, y)dy - полный дифференциал, то из (1.9-1.10) следует
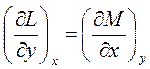(1.11)
Условие (1.11) является необходимым и достаточным, чтобы выражение δA(x, y) было полным дифференциалом. Уравнение (1.11), выражающее свойство коэффициентов полного дифференциала, в применении к функциям состояния называют уравнением Максвелла.
В дальнейшем полный дифференциал будем обозначать знаком d, неполный, т.е. изменение некой величины, не являющейся функцией состояния, - знаком d (например, в случае неполного дифференциала некоторой функции А будем писать δA, в случае полного дифференциала функции А – будем писать dA).
2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
2.1. Формулировка первого закона термодинамики
Первый закон термодинамики гласит, что энергия сохраняется в любом процессе. Математически этот принцип записывается так:
dU = δq - δw,(2.1)
где dU – изменение внутренней энергии системы; δq – теплота, переданная системе окружающей средой; δw – суммарная работа, совершаемая системой над внешними силами. Внутренняя энергия является функцией состояния.
Работа определяется как скалярное произведение вектора силы на вектор перемещения точки приложения силы. При изменении объёма системы, например объёма газа, работа, совершаемая системой против внешнего давления,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.