Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 12

- для обратимого процесса dU – TdS+ pdV = 0.                                                    (3.14)

Условием равновесия (обратимости) процесса, очевидно, является нарушение неравенств (3.13), (3.14) в случае протекания процесса, отклоняющего систему от равновесия.

Таким образом, термодинамический критерий равновесия для закрытых систем можно записать как

δS ≤ δq/T,                                                                    (3.15)

где δ – означает виртуальное (предположительное) изменение термодинамических функций или параметра.

Уравнение (3.15) эквивалентно следующему:

δZ = δU – T δS + p δV ≥0            (3.16)

или

δZ ≥ 0            (3.17)

где

δZ = δU – T δS + p δV(3.18)

(δZ - вводится для удобства записи).

В зависимости от ограничений, накладываемых на систему, её описание целесообразно проводить, оперируя тем или иным набором термодинамических параметров и функций.

1. В частности, если в качестве термодинамических параметров (переменных) используются (S, p), то оперируют с энтальпией

Н = U + pV            (3.19)

                                          (3.20)

Это связано с тем, что в этих координатах с помощью функции энтальпии многие свойства системы можно выразить в явном виде.

В частности, если S, p = const, то  и в качестве критерия равновесия можно рассматривать

                                                             (3.21)

Действительно,

откуда

И, следовательно, в случае p, S = const 

                                                        (3.22)

Т.е. условие равновесия для равновесного (обратимого) процесса:

                                                  (3.23)

Для необратимого процесса:

.

2. Если в качестве термодинамических параметров используются (T, V),то в рассмотрение вводится термодинамическая функция состояния

А = U – TS,                                                        (3.24)

называемая энергией Гельмгольца.

Легко убедиться, что в этом случае при Т, V = const критерием равновесия является

                                                  (3.25)

Для равновесного процесса

(3.26)

                                                      (3.27)

Откуда следует, что при V,T = const

(dA)_{T, V} = 0.                                                                 (3.28)

Из (3.18) с учетом (3.26) следует

.

Или .

3. Если в качестве термодинамических переменных используются (p, T), то вводят термодинамическую функцию состояния

G = U + pV – T S(3.29)

называемую свободной энергией Гиббса

В случае p, Т = const с учетом (3.18)

Отсюда следует, что в случае p,Т = const критерием термодинамического равновесия является

.                                                (3.30)

В случае равновесного (обратимого) процесса

                                  (3.31)

или с учетом (3.14)

                                             (3.32)

откуда для равновесного процесса

.                                                    (3.33)

Замечание. При выводе критериев предполагалось, что работа w связана только с действием давления и изменением объёма системы (dw = pdV). В общем случае могут быть другие виды работ, тогда dw будет другим.

3.3. Политропические процессы

Функции двух переменных: замена переменных, якобианы

Рассмотрим переход от пары независимых переменных (x, y) к паре (x, h). Вводится понятие функционального определителя (якобиана), который обозначается и определяется следующим образом:

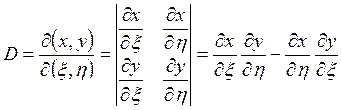                              (3.34)

Геометрический смысл якобиана D заключается в том, что он представляет собой коэффициент изменения элементарной площади при переходе от (x, y) - плоскости к (x, h) - плоскости:

Основные свойства якобианов

1) 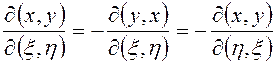                                                                                     (3.35)

(3.35) следует из определения (3.34).

2) 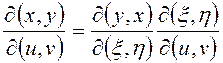                                                                                               (3.36)

Теорема умножения. Вытекает из правил дифференцирования сложной функции.

3) 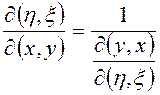                                                                                                            (3.37)