Последнюю формулу зачастую используют при анализе поведения реальных растворов.
Диаграммы, приведенные на рис. 9.2 и 9.3, представляют собой наиболее простые типы диаграмм. Для неидеальных систем, неограниченно смешивающихся в жидкой фазе, часто наблюдаются диаграммы с максимумами или с минимумами, примеры которых приведены на рис. 9.1.
Поведение систем, описываемых диаграммами, изображенными на рис. 9.1 – 9.3, подчиняется ряду закономерностей, называемых правилами Гиббса – Коновалова.
Первое правило Гиббса – Коновалова гласит: в равновесии пар обогащен тем компонентом, прибавление которого к смеси вызывает понижение температуры кипения.
Действительно, рассмотрим, например, диаграмму на рис. 9.2. В ситуации, изображаемой точкой С, система двухфазна и пар обогащен по сравнению с жидкостью вторым компонентом с меньшей температурой кипения. Прибавление второго компонента приводит к увеличению его молярной доли как в жидкой, так и в газообразной фазе. Для сохранения давления в системе необходимо, чтобы изображающая точка из ситуации, описываемой точкой (С), сдвинулась вниз и вправо. Таким образом, температура кипения смеси понижается.
Это правило легко следует и из выражения (8.28). Если
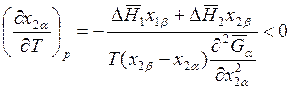, то 
и,
следовательно, содержание второго компонента в паре (β фаза) выше, чем в
жидкости.
Второе правило Гиббса – Коновалова: в точках экстремумов состав пара и жидкости одинаков. Это правило легко вытекает из соотношений типа (8.28):
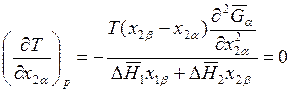, если 
.
Растворы, для которых состав пара и жидкости одинаковы, называются азеотропными. При кипении или перегонке состав азеотропа не меняется, и этот раствор невозможно разделить на чистые компоненты с помощью перегонки.
Из рис. 9.1
видно, чт оесли на диаграмме давление – состав наблюдается максимум, то на
диаграмме температура – состав наблюдается минимум и наоборот. Этот вывод легко
следует из вида выражений (8.26) и (8.29), так как при прохождении через точку
экстремума () знаки производных 
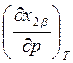и
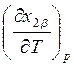меняются противоположным образом.
Третье
правило Гиббса – Коновалова: в изобарических или изотермических условиях состав
обеих фаз меняется в одном направлении, что следует из уравнений (8.28) и
(8.29). Действительно, при изобарическом изменении температуры величины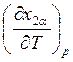 
и 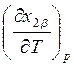имеют
один и тот же знак. Аналогичный вывод следует и из рассмотрения уравнений
(8.25) и (8.26): состав обеих фаз меняется в одном направлении при
изотермическом изменении давления.
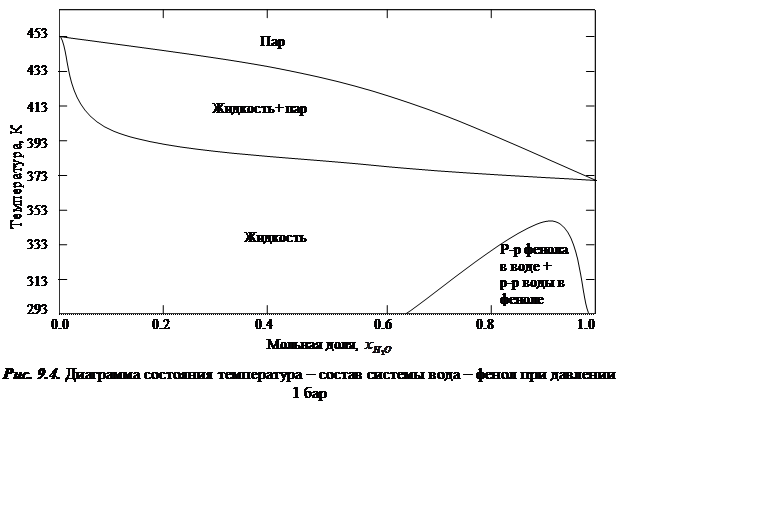
Если в жидком состоянии вещества могут расслаиваться, то это приводит к возникновению более сложных диаграмм, пример которых приведен на рис. 9.4.
Следует отметить, что различие в составе пара и жидкости используется при перегонке жидкостей в целях их разделения.
9.6. Изменение температуры кипения при растворении нелетучего копонента (Эбулиоскопия)
Из опыта известно, что если в жидкости растворен нелетучий компонент, то температура кипения жидкости повышается. Рассмотрим это явление более подробно на примере идеальной системы. Давление пара растворителя в такой системе определяется законом Рауля:
, (9.48)
где х2 – молярная доля растворителя. При кипении давление пара равно 1 бар независимо от того, имеем ли дело с чистым растворителем или с раствором. Следовательно, в соответствии с уравнением (9.48) в случае растворов происходит повышение температуры кипения. Так как р = 1 бар = const при Т = Ткип, то, дифференцируя уравнение (9.48), получаем
.
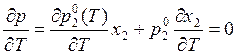Отсюда
.
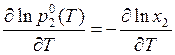Подставляя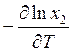 
вместо 
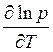в
уравнение Клапйерона – Клаузиуса, получаем
.
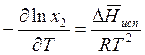Так как х2 = 1 – х1, а х1 – малая величина (будем считать раствор разбавленным), то, принимая, что Т ≈ Ткип, получаем
.
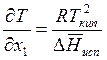Переходя к конечным разностям, последнее уравнение представим в виде
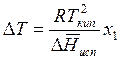. (9.49)
Полученная формула определяет повышение температуры в зависимоти от молярной доли добавленного компонента.
В случае разбавленных растворов (х1 << 1) величину х1 можно определить через моляльность следующим образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.