Другие предметы \ Химическая термодинамика

Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 11

Формулировка второго закона термодинамики

Существует функция состояния, называемая энтропией S, которая определяется, как:

- для любого самопроизвольного обратимого процесса

dS = δq_обр./T, (3.1)

- для любого необратимого процесса

dS > δq/T. (3.2)

Для изолированной системы δq = 0, следовательно, для изолированной системы Sвсегда возрастает (неравновесный процесс) или остаётся равной нулю (равновесный процесс).

Энтропия является мерой необратимости процесса или мерой разупорядоченности системы.

Примеры самопроизвольных необратимых процессов:

1) передача тепла от более горячего тела к более холодному;

2) превращение работы в теплоту (например, в результате трения).

3.1. Равновесие. Стабильность (устойчивость) равновесия

Определение равновесного состояния дано в п.п. 2.1. Иными словами, термодинамическое равновесие – это состояние термодинамической системы, в которое система приходит самопроизвольно в отсутствии внешних воздействий, и из которого система не может выйти без воздействия извне.

Равновесие может быть устойчивым или неустойчивым по отношению к малым или большим возмущениям параметров, характеризующих условие равновесия.

В качестве примеров можно показать следующие различные виды равновесий шара на криволинейной поверхности (рис. 3.1).

Рис. 3.1. Устойчивость равновесия

Для всех случаев, кроме «б» и «в», первая производная y(x) по x, т.е. y_x^¢ = 0.

Случаи «б» и «в» соответствуют системе с дополнительными ограничениями.

Если равновесие системы характеризуется некоторым свойством G(ξ), то условием равновесия, очевидно, является следующее

(3.3)

Это условие можно заменить на

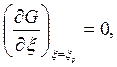(3.4)

где x - это один из параметров, по которому возможно отклонение от равновесия (переменная, от которой зависит G).

Условие (3.4) можно использовать как условие равновесия, но не устойчивости.

Если DG = G – G_равн - малые отклонения, то можно утверждать, что, если

DG > 0 – равновесие устойчивое, (3.5)

DG = 0 – равновесие нейтральное, (3.6)

DG < 0 – равновесие неустойчивое. (3.7)

Если G не имеет разрыва, то, разложив G в ряд Тейлора в окрестности точки равновесия, получим

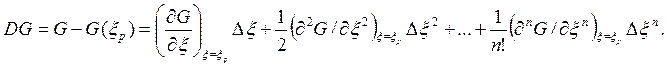(3.8)

Опираясь на условия (3.5 – 3.7), можно показать, что, так как всегда, то условием устойчивого равновесия является

(3.9)

Равновесие является нестабильным, если имеет место обратное неравенство. Если то необходимо исследовать производные более высокого порядка. Если а 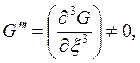то равновесие неустойчивое, т.к. всегда можно найти с таким знаком, чтобы было DG < 0.