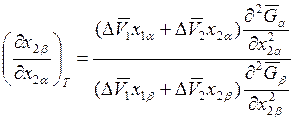Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 31

.                           (8.27)

Если р = const, то

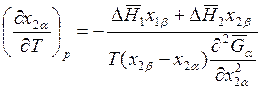;                                             (8.28)

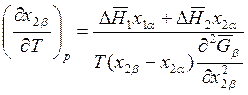;                                                (8.29)

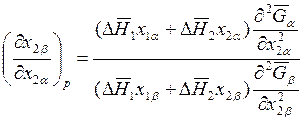.                         (8.30)

Необходимо отметить, что в уравнениях (8.22) – (8.30) использованы парциальные молярные величины и реальные давления. Однако можно построить и иной подход к описанию кривых фазового равновесия с использованием понятий активности и стандартных молярных величин.

Ранее в п. 5.5 были рассмотрены два подхода к определению химических потенциалов конденсированных тел, основанных на введении понятий стандартного состояния и состояния сравнения. В принципе, можно использовать оба подхода. Однако применение уравнения (5.74) более удобно, так как фазовые равновесия обычно исследуются в широких диапазонах концентраций, на концах которых находятся чистые вещества, для которых величины активности можно принять равными единице. Таким образом, химические потенциалы μ_iα и μ_iβ запишем в соответствии с (5.74). Приравняв их, получим

или

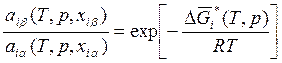,                                         (8.31)

где

.

Уравнение (8.31) описывает равновесие в интегральной форме. Чтобы получить из него уравнение в дифференциальном виде, возьмем дифференциал от обеих его частей, предварительно перейдя к логарифмической форме:

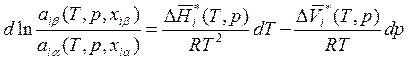,                            (8.32)

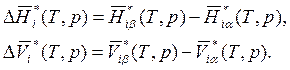
Напомним, что величины  и  представляют собой стандартные изменения энтальпии и объема для чистых веществ в условиях Т = Т(системы) и р = р(системы). Поэтому они не зависят от состава.

Интегрируя выражение (8.32), получаем

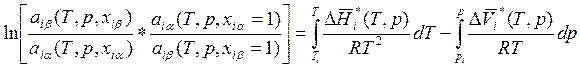,                  (8.33)

где Т_i и р_i – некоторые выбранные за начало отсчета температура и давление. При изучении равновесий жидкость – пар обычно в качестве температуры Т_i берут ту температуру, при которой давление паров над чистой i-й жидкостью равно заданному р, а в качестве давления р_i берут давление насыщенных паров над чистой жидкостью при заданной температуре Т. Величины активностей для чистых веществ обычно полагают равными единице. Таким образом, уравнение (8.33) можно записать так:

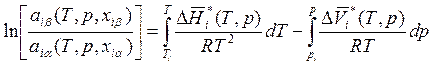.                                   (8.34)

Последнее уравнение позволяет рассчитывать зависимости состава фаз от температуры при р = const и от давления при Т = const. Отметим, что правовая часть (8.34) не зависит от состава. Следовательно, и отношение активностей компонента в обеих фазах не зависит от состава. Примеры, иллюстрирующие применение этого подхода, будут приведены в следующей главе.

9. ТЕРМОДИНАМИКА РАСТВОРОВ

Данная глава посвящена описанию термодинамики и ряда свойств жидких и твердых растворов. Для этого вида смесей характерна возможность сосуществования с газовой фазой, и поэтому их поведение обладает рядом специфических особенностей, что и позволяет выделить данное рассмотрение в отдельный раздел. Изложение материала проведено в основном на примере жидких растворов. Однако это не исключает приложения основных выводов и к твердым растворам, для которых установление равновесий осуществляется, конечно, намного медленнее, чем в жидкости из-за малой подвижности вещества в твердой фазе. Особенно важны такие приложения для твердых растворов, получаемых при затвердевании жидких расплавов, соосаждения или сокристаллизации из жидких растворов и т.д.

9.1. Классификация растворов

Общепринята следующая классификация растворов на основе представлений об избыточных термодинамических функциях:

1. идеальные растворы

,          ,           ;

2. регулярные растворы

,          ,           ;

3. атермальные растворы

,          ,           ;

4. реальные растворы

,          ,           , где  - избыточная молярная функция смешения (отклонение реальной величины от величины функции смешения для идеальной системы) . Черта сверху означает парциальное мольное свойство.

В литературе можно встретить также понятие «совершенный раствор» - это раствор, идеальный при всех концентрациях. Регулярные растворы состоят из веществ, молекулы которых имеют близкие размеры; атермальные – наоборот, содержат молекулы с резко различающимися размерами (например, растворы полимерных молекул и т.д.).