Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 34

Построение фазовых диаграмм двухкомпонентных жидких растворов предполагает нахождение кривых фазового равновесия жидкость – пар. Для описания фазовых диаграмм температура – состав и давление – состав двухкомпонентных жидких растворов удобно использовать формулу (8.34), которая в явной форме включает в себя коэффициенты активности. Как и ранее, будем считать, что индекс «β» относится к паровой фазе (п), а «α» - к жидкой (ж). Найдем зависимости Т(х_2п) и Т(х_2ж) при р = const, а также р(х_2п) и р(х_2ж) при Т = const.

Из (8.34)

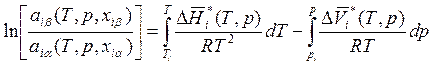,                       (9.19)

тогда при р = const

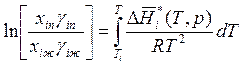.                                   (9.20)

Полагая в выражении (9.20) i = 1 или 2, находим

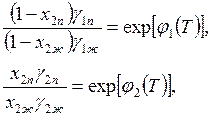                                          (9.21)

где

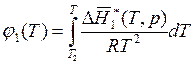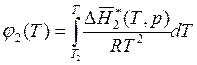,                    ,                    (9.22)

а Т₁ и Т₂ – температуры, при которых давление насыщенных паров над обеими чистыми жидкостями равно заданной величине р.

Если величины γ известны при различных температурах и давлениях, то уравнения (9.21) удобно преобразовать к такой форме:

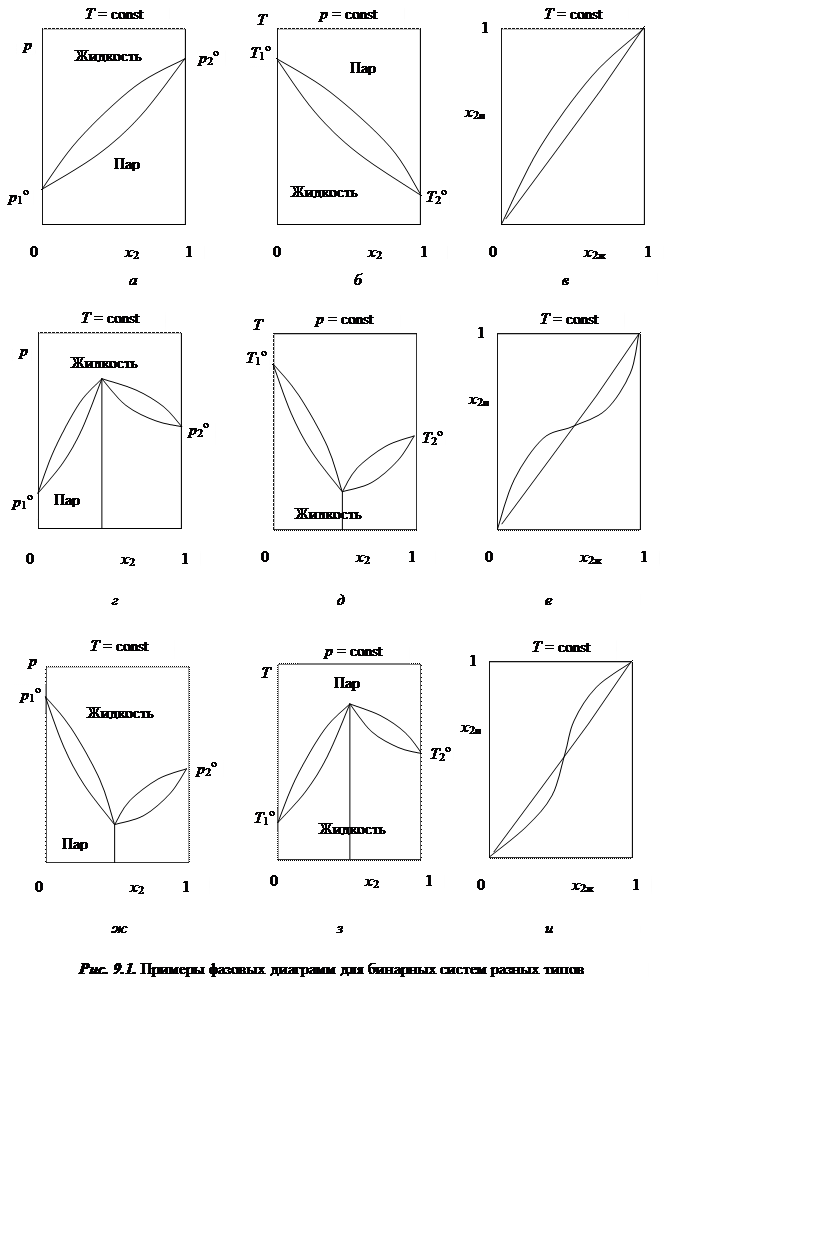
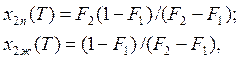                                                            (9.23)

где

,                   .

Используя уравнения (9.23), можно построить кривые жидкости и пара.

Рассмотрим теперь случай Т = const. Тогда из уравнения (9.19) получим

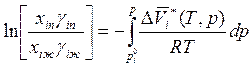,                                             (9.24)

где  - давление паров над i-й чистой жидкостью, а р – полное давление насыщенных паров над смесью.

Из выражения (9.24) находим

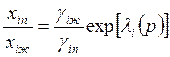,                                                 (9.26)

где введено обозначение

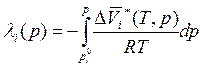.                                          (9.27)

Если зависимости γ_iα и γ_iβ от Т и р известны, то можно написать следующую систему уравнений:

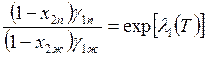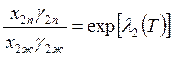,                  .            (9.28)

Отсюда получаем уравнения для х_2п и х_2ж:

,             ,                 (9.29)

где

,                   .

Если паровая фаза идеальна и молярным объемом жидкой фазы можно пренебречь, то

,                       .                                  (9.30)

Подставляя уравнения (9.30) в выражения (9.29), получаем

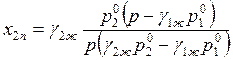,                                                (9.31)

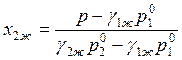,                                                           (9.32)

Из выражения (9.31) следует уравнений для кривой пара

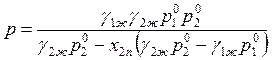                                          (9.33)

из выражения (9.32) следует уравнение для кривой жидкости

.                                         (9.34)

Если жидкая фаза также идеальна, то

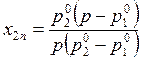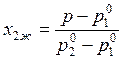,                   .                                  (9.35)

Из уравнений (9.35) получаем выражения для кривых пара

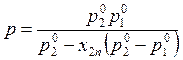                                               (9.36)

и жидкости

.                                              (9.37)

Уравнения (9.36) и (9.37) позволяют установить связь между х_2п и х_2ж при Т = const:

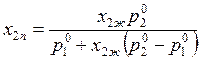.                                           (9.38)

Уравнения (9.31 – 9.32) и (9.38) легко получаются и исходя из закона Рауля, записанного в виде выражения (9.3).

Рассмотрим более подробно свойства фазовых диаграмм жидких бинарных растворов, которые могут неограниченно смешиваться при любых молярных соотношениях. В качестве примера на рис. 9.2 приведена диаграмма температура – состав для системы толуол – бензол при фиксированном давлении 53,3_*10³ Па (400 торр). Кривые фазового равновесия построены по формулам (9.23) в предположении идеальности системы. Эти кривые очень близки к экспериментальным. Видно, что обе кривые образуют фигуру, называемую «линзой» («сигарой» или «рыбкой»).

Если термодинамическое состояние соответствует точке А, расположеной над кривой пара (рис. 9.2), то система находится только в парообразном состоянии. В соответствии с правилом фаз у нее три независимых степени свободы, например, р, Т и х₂. Ниже кривой жидкости (точка G) система находится только в жидком состоянии. В этом случае она обладает также тремя степенями свободы.

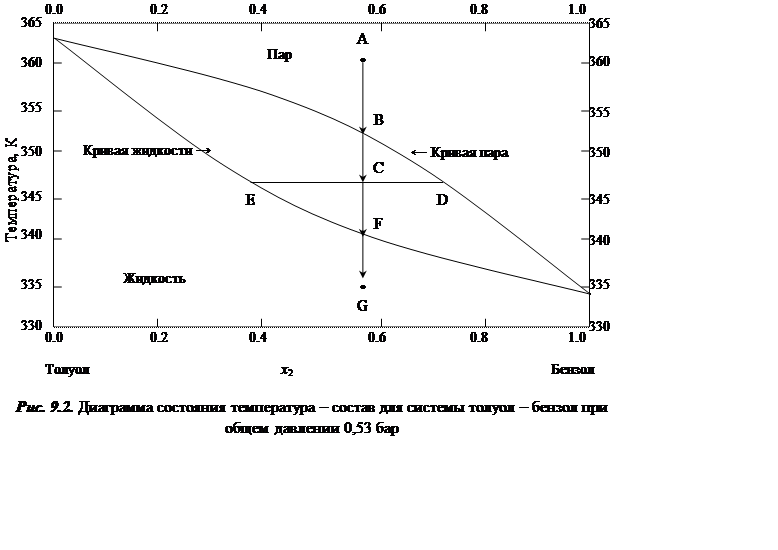
Представляет интерес область, заключенная между кривыми жидкости и пара. Для описания этой области рассмотрим последовательное охлаждение исходной газообразной системы, состояние которой изначально описывается точкой А. По мере охлаждения системы изображающая точка двигается сначала вертикально вниз до пересечения с кривой пара – точка В.