Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 32

9.2. Давление пара над растворами. Закон Рауля

Рассмотрим раствор двух веществ – 1 и 2, находящихся в равновесии с газовой фазой. Равновесие жидкой и газовой фаз определяется равенством химических потенциалов обоих веществ в обеих фазах – жидкой (ж) и паровой (п):

,       (i = 1, 2).

Поэтому в общем случае неидеального раствора можно записать

и

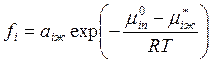.                                                     (9.1)

Соотношение (9.1) должно выполняться и для чистого i-го компонента, для которого

,          .

Это позволяет определить величину :

.

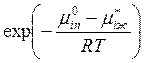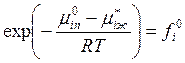Следовательно, значение летучести i-го компонента над раствором определяет соотношение

.                                                                   (9.2)

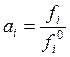
В случае идеальной газовой смеси над раствором:

,           ,        

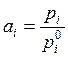
это один из способов определения активности веществ в растворе.

Введя коэффициенты летучести и активности, из (9.2) получаем

, где  и  характеризуют коэффициенты летучести и активности i-го компонента в паровой и в жидкой фазах соответственно. Отсюда

.

Если газовая фаза идеальна, то

и

.

Если обе фазы идеальны, то

.                                                                   (9.3)

Величина  зависит в принципе от суммарного внешнего давления, но этой зависимостью очень часто можно пренебречь. Следовательно, в идеальных системах парциальное давление i-го компонента в насыщенном паре над конденсированной смесью пропорционально его молярной доле в конденсированной фазе. Эта формулировка определяет закон Рауля. Полное давление равно сумме парциальных давлений всех компонентов:

.

Существует и частная формулировка закона Рауля для случая, когда один из компонентов является нелетучим. В этой ситуации полное давление пара в системе определяется только давлением пара растворителя, которое зависит от его молярной доли в соответствии с формулой (9.3). Считая, что молярная доля растворителя в жидкой фазе равна x₂, легко можно записать:

или

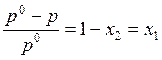,                                                   (9.4)

где х₁ – мольная доля нелетучего компонента в жидкой фазе. Таким образом, относительное уменьшение давления пара над жидкостью равно молярной доле нелетучего компонента. Это – вторая формулировка закона Рауля, имеющая важное, но более частное значение.

Закон Рауля в широком диапазоне концентраций хорошо выполняется только для молекул с близкими структурами, например, смеси бензола и толуола.

9.3. Растворимость газа в жидкости. Закон Генри

Рассмотрим процесс растворения газа в жидкости. В равновесии для растворяющегося компонента выполняется равенство

μ (в газ. фазе) = μ (в жидк. фазе).

Химический потенциал растворяемого газового компонента в рассматриваемых фазах равен

,                , где а_i – активность растворенного газа i в жидкости. Приравнивая химические потенциалы, получаем

.                                               (9.5)

Отсюда

.                                                                   (9.6)

Параметр К_Г – называют константой Генри:

.

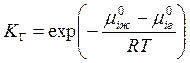Выражение (9.6) представляет собой закон Генри.

В идеальной системе концентрация растворенного газа в конденсированной фазе пропорциональна парциальному давлению газа над раствором. Действительно, в этом случае

и          .

Тогда

,                                                                  (9.7)

где х_i – молярная доля газа i в жидкости, р_i – парциальное давлениерастворенного газа i над жидкостью. Выражение (9.7) применимо и к реальным растворам, но при малых парциальных давлениях растворяющегося газа, когда отличием коэффициента активности от единицы для растворенного газа можно пренебречь.

Зачастую закон Генри записывают также следующим образом:

,                                                                  (9.8)

где С_i – концентрация газа i в жидкости, например, в единицах моль/л.

Следует отметить особенности использования величины  в формуле (9.5). Коэффициент активности растворенного вещества стремится к единице при малых концентрациях этого вещества, что позволяет определить величину  непосредственно из уравнений (9.5) и (9.6) так: