Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 17

где α = (1/V)·(∂V/∂T)_р , β = (-1/V)·(∂V/∂р)_T  - коэффициенты термического расширения и сжатия.

Основные термодинамические соотношения для многокомпонентных, гомогенных открытых систем приведены в табл. 5.1.

Таблица 5.1

Дифференциальные уравнения	Интегральные уравнения	Уравнения Гиббса-Дюгема при Т и p = const

Дополнительные соотношения для химического потенциала

                   

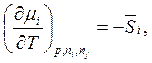
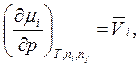
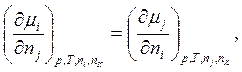
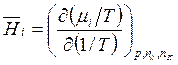                                   (5.39)

Парциальные свойства можно выразить через мольные функции состояния и мольные доли x_i = n_i /N , N – общее число молей реакционной смеси.

Например

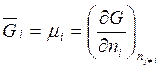.                                                   (5.40)

Учитывая, что  ( – мольная энергия Гиббса), и производя замену переменных (n₁, n₂, ……n_j, …n_r) → (n, x₂, …x_r), можно получить

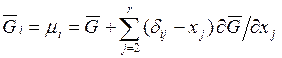                            (5.41)

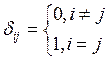где символ Кронекера, , или 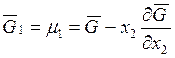, если система двухкомпонентная.

Задание. Выразите для трехкомпонентного раствора.

5.4. Соотношения для химического потенциала

Термодинамические движущие силы и условия равновесия задаются через химические потенциалы в предложении, что известна функциональная зависимость химического потенциала от состава.

Однако, определение таких зависимостей весьма сложная задача.

Понятия летучести и активности тесно связаны с вопросом описания химических потенциалов реальных газов, растворов, сплавов.

5.4.1. Химический потенциал чистого идеального газа

При постоянной температуре для чистого компонента  (см. табл.5.1.) и, следовательно,

,                                                        (5.42)

где  – мольный объём газа,  – парциальное давление газа.

В случае идеального газа

                                                                   (5.43)

следовательно,

                                                   (5.44)

Интегрируя от (стандартное состояние) до  при температуре Т, получаем

                             (5.45)

Обычно, р⁰ = 1 атм, тогда можно записать так

,                                           (5.46)

где m⁰(T) – функция только температуры; р – относительное давление, численно равное давлению, измеряемому в атм.

Заметим, что (5.46) и (5.43) эквивалентны.

5.4.2. Химический потенциал чистого реального газа. Летучесть

Уравнения состояния реальных газов сложны. Поэтому, если их использовать вместо (5.43), то соотношения для m  получить невозможно в простом виде.

Для описания химических потенциалов реальных газов вводят понятие летучести на основе соотношения [сравните с (5.44)]

                                                               (5.47)

где f – летучесть рассматриваемого чистого газа.

Интегрируя от до p, при (T = const), будем иметь

                                            (5.48)

где р⁰ – стандартное состояние, выбранное так, что f⁰= 1. В этом случае можно записать

                                                (5.49)

(f – безмерная величина). Стандартным обычно считают идеальный газ р⁰ = 1атм. Поэтому принимается, что f⁰ =1 (для идеального газа при р = 1 атм).

Уравнения (5.44), (5.47), (5.46) и (5.49) очень похожи. Если газ идеален, то f = р/(1 атм). При таком подходе проблема описания химического потенциала сводится к проблеме определения зависимости f (р).

В принципе понятие летучести может быть полезно и при описании жидкостей и твёрдых тел, но так как мольный объём жидкости и твёрдого вещества в 1000 раз меньше, чем у газов, то здесь влияние давления на химический потенциал может проявляться только при очень высоких р, поэтому в этом случае использование летучести, как правило, не целесообразно.

5.4.3. Химические потенциалы газовых смесей

При описании смесей обычно оперируют с парциальными величинами (парциальные давление р_i, объём V_i и.т.д.).

Например,

          -  идеальный газ.

Для смеси газов летучесть вводится аналогично, как это делали для чистого газа, на основе изотермического уравнения

                                                (5.50)

После интегрирования