Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 25

7.4. Существование двух фаз. Уравнение Клаузиуса-Клапейрона (однокомпонентные системы)

В состоянии равновесия [см. (7.7)]

 (см. табл. 3.1) →                                            (7.12)

                                                (7.13)

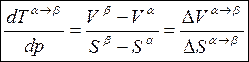                                                          (7.14)

где  – молярные объёмы; S^α, S^β – молярные энтропии.

Это уравнение Клаузиуса-Клапейрона, выражающее зависимость температуры фазового перехода α → β от давления.

При плавлении и перекристаллизации , поэтому dT/dр мало, так dT/dр ≈ 0,004 К/атм (плавление серебра) – мало.

При испарении на несколько порядков выше, поэтому dT/dр ≈ 28,1 К/атм (вода) –велико.

Учитывая, что в соответствии с (7.11)  (7.14)→

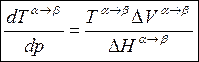                                                           (7.15)

Значения стандартных мольных величин ΔН и ΔS некоторых веществ для процессов плавления и испарения приведены в таблице. Видно, что изменение значений теплоты и энтропии при испарении гораздо больше соответствующих изменений при плавлении.

Таблица 7.1

Для фазовых переходов плавления и испарения существует ряд простых эмпирических закономерностей, позволяющих оценивать энтропию и энтальпию перехода, зная лишь температуру фазового перехода (правило Трутона). Для неполярных жидкостей

,             Дж/(моль К)

или

,                          Дж/(моль К).

Для простых веществ

,                                Дж/(моль К).

Для неорганических веществ

,                               Дж/(моль К).

Для органических веществ

,                             Дж/(моль К).

Параметры ΔН и ΔS даже для идеальных систем зависят от температуры и давления. Поэтому уравнение (7.15) нельзя проинтегрировать в явном виде. В связи с этим рассмотрим некоторые частные случаи.

Фазовый переход конденсированное вещество – пар

В случае фазового перехода жидкость-пар вдали от критической точки (относительно низкие давления).

.

Следовательно, (7.15)

.

В случае идеального газа

или

.

Полагая, что 

.                                                (7.16)

Здесь Т_кип соответствует температуре кипения при р = 1атм. Это константа интегрирования: Т = Т_кип при р = 1 атм.

Уравнение (7.16) выражает зависимость давления фазового перехода жидкость/пар от температуры.

Задание. Температура льда открытого катка –2,5 ⁰С. Рассчитать минимальное давление (например, конька), которое необходимо, чтобы расплавить лёд.

Дано. При 0 ⁰С  V^ж = 1 дм³/кг, V^тв. = 1,09 дм³/кг, теплота плавления ∆Н = 333 кДж/кг.

Указание. Воспользоваться уравнением Клаузиуса-Клапейрона (проинтегрировать от р = 1 атм до р, Т = 270,5 К до 273К).

Фазовый переход конденсированное вещество – конденсированное вещество (без участия газовой фазы)

К процессам такого типа относятся фазовые переходы твердое вещество – твердое вещество, твердое вещество – жидкое вещество, жидкое вещество – жидкое вещество. Примером фазового перехода твердое вещество – твердое вещество могут служить аллотропные превращения одной кристаллической модификации в другую:

S (ромбическая) = S (моноклинная)

Примером фазового перехода твердое вещество – жидкое вещество могут служить процессы плавления.

Для описания таких равновесий используется уравнение Клаузиуса-Клапейрона в форме выражения (7.15). С его помощью можно получить кривую сосуществования двух фаз, если известны зависимости молярных величин ΔН и ΔV от температуры и давления. Если изменения параметров (Т и р) невелики, то можно считать величины ΔН и ΔV постоянными и равными их значениям при стандартных условиях. В этом случае кривая сосуществования двух фаз описывается уравнением