Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 33

.

Величина  описывает изменение энергии Гиббса одного моля растворяемого газообразного вещества при переходе из газовой фазы в жидкую.

9.4. Предельно разбавленные растворы

В очень разбавленных растворах исчезает взаимодействие между молекулами растворенного вещества (но, естественно, не между молекулами растворителя и растворенного компонента). Поэтому можно полагать, что все растворы при сильном разбавлении становятся идеальными по отношению к растворенному соединению.

Интересно установить характер зависимостей термодинамических величин от молярной доли компонента, присутствующего в системе в малом количестве (х₂). Из обобщенного уравнения Гиббса-Дюгема (5.35) при постоянных р и Т для i = 1, 2 (бинарная смесь) следует

.

Откуда

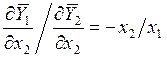,                                                  (9.9)

где  и  - любые парциальные молярные величины. Видно, что при

.

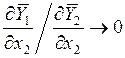Для выполнения последнего соотношения необходимо

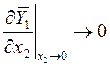  и 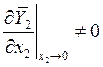                                    (9.10)

ил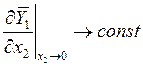и

       и 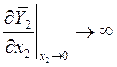         .                        (9.11)

Рассмотрим, какие термодинамические величины удовлетворяют соотношениями (9.10), а какие (9.11). Для этого обратимся к идеальным двухкомпонентным системам.

Величины парциальных энергий Гиббса определяются соотношениями

,                      .                 (9.12)

Дифференцируя оба уравнения по х₂ и устремляя к пределу при х₂ → 0, получаем

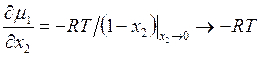,                               (9.13)

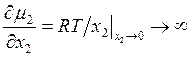.                                             (9.14)

Итак, μ₁ и μ₂ подчиняются соотношению (9.11). При малых значениях х₂ для μ₁ и μ₂ будем иметь

,                      .                 (9.15)

Рассмотрим энтропию. Учитывая (9.12), можно записать

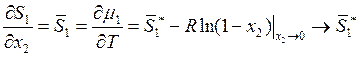,                       (9.16)

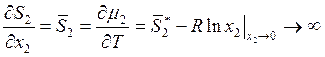,                              (9.17)

где  и  - энтропии чистых жидкостей. Следовательно, энтропия также относится к случаю, описываемому уравнениями (9.11). При малых значениях х₂ в первом приближении

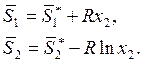                                            (9.18)

Реально, как показывают эксперименты, растворы неэлектролитов можно считать идеальными, если , а в случае изотоп-замещенных молекул практически при любом значении х₂. Что касается растворов электролитов в воде, то для них условия идеальности выполнены лишь при .

В случае энтальпии уравнение (9.9) неприменимо к идеальным растворам, т.к. величины  и  не зависят от х₂. В неидеальных системах величина  - энтальпии растворения при бесконечном разбавлении. Величина , т.к. малые добавки второго компонента не сказываются на величине . Следовательно, энтальпия удовлетворяет соотношению (9.10). Аналогичным образом можно рассмотреть и другие величины.

9.5. Фазовые диаграммы двухкомпонентных жидких растворов. Равновесие жидкость – пар. Полная смешиваемость в обеих фазах

Для наглядного отображения свойств жидкости и пара в бинарных смесях обычно строят диаграммы трех типов (рис. 9.1):

1. равновесное давление пара – состав при Т = const (рис. 9.1, а, г, ж);
2. равновесная температура – состав при р = const (рис. 9.1, б, д, з);
3. равновесный состав газа – равновесный состав жидкости при Т = const (рис. 9.1, в, е, и).

Необходимо отметить, что координату х₂ обычно приписывают веществу с более высоким давлением пара или с более низкой температурой кипения. Для диаграмм первых двух типов вдоль оси абсцисс откладывают одновременно молярную долю второго вещества в паре - х_2п и в жидкости - х_2ж.

На диаграммах температура – состав кривая пара Т(х_2п) описывает зависимость равновесной температуры от состава пара при фиксированном давлении пара, а кривая жидкости Т(х_2ж) описывает зависимость равновесной температуры системы от состава жидкой фазы при том же постоянном значении давления пара. В этом случае кривая пара проходит выше кривой жидкости.

На диаграммах давление – состав кривая жидкости р(х_2ж) описывает зависимость равновесного давления пара от состава жидкости при фиксированной температуре всей системы, а кривая пара р(х_2п) описывает зависимость равновесного давления пара от состава паровой фазы при той же фиксированной температуре. В этом случае, наоборот, кривая жидкости лежит выше кривой пара.