Другие предметы \ Химическая термодинамика

Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 24

Согласно Эренфесту

• Фазовый переход первого рода – это равновесный переход вещества из одной фазы в другую, при котором скачком изменяются первые производные от энергии Гиббса G по Т и р (рис. 7.1.).

Следовательно, при фазовом переходе первого рода скачком изменяется S и V, так как

S = -(∂G/∂T)_р, V = (∂G/∂р)_T.

В системах с фазовым переходом первого рода могут существовать метастабильные состояния. Все обычные фазовые переходы - это первого рода.

• Фазовый переход второго рода – это равновесный переход, при котором скачком изменяются только вторые производные от G (рис. 7.2.).

; ; .

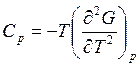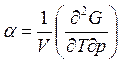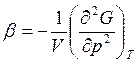Здесь G изменяется непрерывно – излома нет. Метастабильные состояния невозможны.

Примеры фазового перехода второго рода – переход жидкого гелия в сверхтекучее состояние, железа из ферромагнитного в парамагнитное состояние, металла из обычного в сверхпроводящее и др.

Рассмотренные законы термодинамики позволяют определять условия существования различных фаз, если система находится в состоянии термодинамического равновесия, или является ли та или иная фаза устойчивой при заданных термодинамических параметрах, например, (р, Т) или других, выбранных для описания системы.

7.2. Стабильность фаз в однокомпонентных системах

При заданных р и Т для анализа устойчивости фаз в качестве функции состояния (характеристической функции) удобно использовать энергию Гиббса (см. раздел 3.2)

. (7.1)

При р, Т=const было установлено, что условием равновесия системы является

. (7.2)

Это означает, что при любых заданных р и Т система находится в равновесии, если

. (7.3)

Отсюда, если при данных Т и р вещество может иметь структуру α или β (образовывать фазу α и β), то α более стабильна, чем β, если

. (7.4)

При других р и Т условие (7.4) может измениться на противоположное, соответственно, тогда в новых условиях β будет устойчивее α.

Таким образом, для практических расчётов устойчивости необходимо знать зависимость G (р, T) для каждой фазы.

Эту информацию, как правило, можно получить из справочных термодинамических таблиц.

Величину G невозможно определить абсолютно, но этого и не требуется, так как всегда интересует отклонение (изменение) G, поэтому в справочниках обычно даётся величина

G - H₂₉₈⁰ (Дж/моль) (G =H - TS).

На рисунке 7.3. показан пример изменения от температуры для цинка. Необходимо обратить внимание, что на этой кривой в точке фазовых превращений отсутствует разрыв

G_тв = G_ж,G_ж = G_газ.

Наклон кривой G(T) всегда отрицателен, так как (см. уравнение Максвелла)

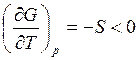. (7.5)

Кривая G(T) выгнутая, так как

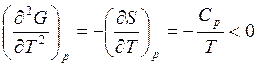. (7.6)

Выражение (7.6) получено из (2.6), (3.1) с учетом, что H = U + pV, и следовательно,

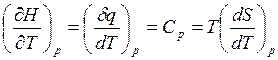Интересно отметить другие свойства энергии Гиббса. Так

(∂G/∂р)_T = V > 0 – положительный наклон G(р)

(∂²G/∂р²)_T= (∂V/∂р)_T= -βV < 0 –отрицательная кривизна G(р) (см. рис. 7.4).

На рис. 7.4. показаны зависимости G (T) для алмаза (кривая 1) и графита (кривая 2). Алмаз и графит – это различные фазы углерода. Их отличие состоит в кристаллической структуре.