В этой точке система становится двухфазной, хотя количество жидкой фазы пока близко к нулю. Последующее понижение температуры, например до величины в точке С, происходит в двухфазной области. Здесь система имеет две термодинамические степени свободы. Изображающая точка С не отвечает реальному состоянию системы.
Чтобы найти состав каждой фазы ,через точку С проводят прямую, параллельную оси абсцисс, до пересечения с границами области в точках Е и D. Состав пара соответствует величине абсциссы х2(D), а жидкости - х2(Е). Отрезок ЕD, представляющий собой часть прямой, проведенной параллельно оси абсцисс через фигуративную точку до пересечения с ближайшими линиями кривых фазового равновесия, ограничивающими область с фигуративной точкой, называется нодой (или коннодой). Величина абсциссы в точках Е и D соответствует составу жидкой (точка Е) и газовой (точка D) фаз. Фигуративная точка, характеризующая газовую фазу, движется вдоль кривой пара, а фигуративная точка жидкой фазы движется вдоль кривой жидкости.
Пользуясь диаграммой, наряду с составом отдельных фаз в точке С можно определить и относительное количество каждой из фаз.
Предположим, что количество вещества в исходной газообразной системе (точка А) равно одному молю. Тогда количество второго компонента равно х2(А) или, что то же самое, х2(С), где х2(С) – значение абсциссы в точке С. При охлаждении системы до температуры, соответствующей точке С, количество газовой фазы будет равно некоторой величине, которую обозначим через nп, а ее состав будет определяться величиной абсциссы в точке D. Количество жидкой фазы обозначим через nж, а ее состав будет определяться величиной абсциссы в точке Е. Учитывая, что общее количество молей вещества в обеих фазах равно единице и что количество второго компонента в обеих фазах равно х2(С), получаем следующую систему уравнений:
![]() , (9.39)
, (9.39)
![]() . (9.40)
. (9.40)
Из этой системы легко найти, что
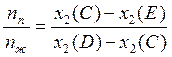 . (9.41)
. (9.41)
Полученная формула отражает правило рычага: отношение числа молей пара и жидкости равно отношению длин отрезков, на которые изображающая точка С делит ноду ЕD.
Правило рычага применимо не только к рассмотренной диаграмме, а вообще к диаграммам самых различных типов, в котрых имеются кривые фазового равновесия, выделяющие двухфазные области.
Перейдем к рассмотрению диаграмм давление – состав для бинарных жидких растворов. В качестве примера на рис. 9.3 изображена рассчитанная фазовая диаграмма той же системы толуол – бензол в предположении идеальности и при фиксированной температуре, равной 41 0С. Из рисунка видно, что даже в случае идеальных растворов состав газовой фазы может не совпадать с составом жидкой фазы. Состав обеих фаз совпадают только тогда, когда в идеальной системе
![]() .
.
Моделью идеального раствора может служить жидкая или твердая смесь молекул, близких по составу и строению, например, смесь С6Н6 с С6Н5D и т.п. На практике по-настоящему идеальные растворы встречаются редко.
Изложенная теория фазовых диаграмм для растворов достаточно удобна на практике, если известны зависимости коэффициентов активности от состава, температуры и давления. Если эта информация отсутствует, то необходимо использовать общую теорию двухфазных систем.
Для изучения
поведения полного давления неидеальных растворов можно воспользоваться
уравнением (8.25). Величина ![]() для идеальной смеси
равна
для идеальной смеси
равна
![]()
зная, что ![]()
![]() , (9.42)
, (9.42)
откуда для 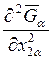 получаем
получаем
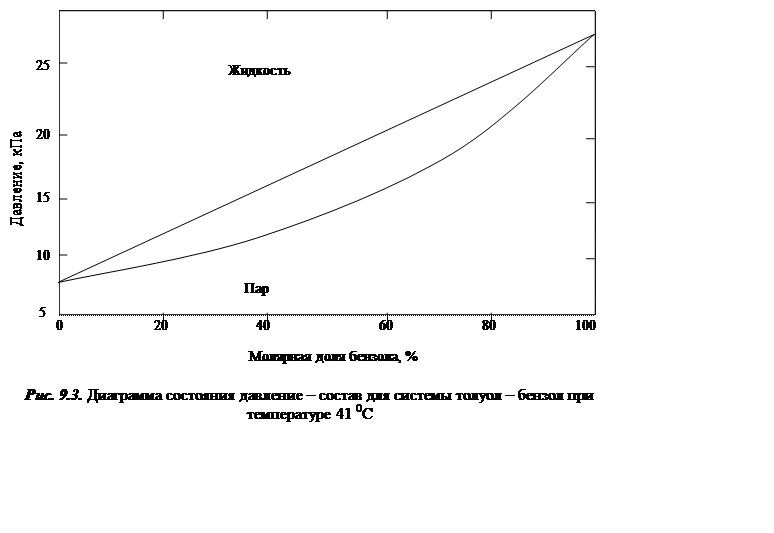
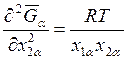 . (9.43)
. (9.43)
Считая, что газовая фаза
идеальна, для величины 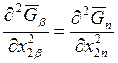 в соответствии с
выражением (9.43) получаем
в соответствии с
выражением (9.43) получаем
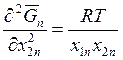 . (9.44)
. (9.44)
Величины ![]() в
пренебрежении объемом жидкой фазы равны
в
пренебрежении объемом жидкой фазы равны
![]() (i = 1, 2). (9.45)
(i = 1, 2). (9.45)
Подставляя формулы (9.44) и (9.45) в выражение (8.26), получаем
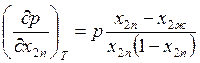 , (9.46)
, (9.46)
или
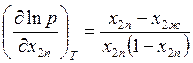 , (9.47)
, (9.47)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.