где pi - внешнее давление (задается суммарным весом грузиков, которыми нагружен поршень); DVi – изменение объёма при снятии одного грузика.
Теперь проведём обратный процесс –
поршень будем постепенно нагружать гирьками и тем самым будем сжимать газ.
Процесс сжатия газа изобразится верхней ломаной линией NM
(рис. 1.2, а). Площадь между нею и осью абсцисс будет равна работе w3, затраченной на сжатие газа. Из рис. 1.2 (а)
следует, что w3 > wп. Разность (w3
- wп) будет равна площади, заключённой
между верхней и нижней ломаными линиями.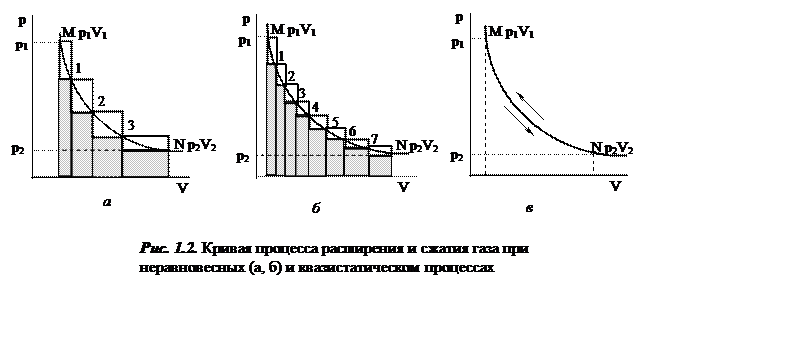
Проведём процесс расширения и сжатия газа в цилиндре по-иному: величину каждого грузика уменьшим, а их число увеличим, например, вдвое. При этом начальное и конечное общее внешнее давление останется неизменным. Увеличится число точек на ломаной линии MN, отвечающих состояниям равновесия (М, 1, 2, 3, 4, 5, 6, 7, N). Возмущение равновесия при каждом шаге уменьшиться, а число шагов увеличится. Полученная работа, как это следует из рис. 1.2 (б), при этом несколько увеличится, а затраченная на сжатие газа работа, наоборот, уменьшится. Уменьшится и разность (w3 – wп). Из рассмотренных здесь двух процессов расширения и последующего сжатия газа вытекает: если внешнее давление изменяется на бесконечно малую величину dp, то ломаные линии прямого и обратного процессов практически совпадут с линией MN (рис. 1.2, в). Полученная работа при расширении газа будет максимальной, а затраченная работа при сжатии газа - минимальной. Их разность (w3 – wп) будет стремиться к нулю. Число точек на линии MN (рис. 1.2, в), отвечающих промежуточным состояниям равновесия, будет бесконечно большим. Отсюда процессы сжатия и расширения газа при последних условиях его проведения окажутся бесконечно медленными и практически непрерывно будут проходить через состояния, бесконечно близкие к равновесным, что отвечает определению равновесного процесса. Предельно замедленный процесс называется также квазистатическим процессом*. Если квазистатический процесс провести сначала в прямом направлении, а затем в обратном (рис. 1.2, в) через те же равновесные состояния, то не обнаружится никаких изменений как в самой системе, так и в окружающей среде; процесс проведён без потерь: w3 = wп. Такой процесс называется термодинамически обратимым.
При квазистатическом процессе сумма в уравнении (1.1) может быть заменена интегралом:
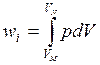 (1.2)
(1.2)
dwп = p dV (1.3)
Внешнее давление при квазистатическом процессе на бесконечно малую величину dp отличается от внутреннего давления в системе, которое может быть вычислено из уравнения состояния, например, для идеального газа [уравнения состояния Менделеева-Клапейрона (1.5)]. Уравнение (1.2) позволяет вычислить работу расширения при различных квазистатических процессах. Понятия равновесного и обратимого процессов широко используются при термодинамических исследованиях и, в частности, при изучении химического равновесия.
Реальные процессы (рис. 1.2, а, б) являются неравновесными и необратимыми w3 – wп ≠ 0. Величину работы необратимого процесса можно определить путём прямого измерения. Иногда реальные процессы можно рассматривать в приближении равновесных.
Адиабатный процесс – процесс, при котором система не получает теплоты извне и не отдает ее.
Изохорный процесс – процесс, происходящий при постоянном объеме системы.
Изобарный процесс – процесс, происходящий при постоянном давлении в системе.
Изотермический процесс – процесс, происходящий при постоянной температуре системы.
Уравнение состояния системы – функция, устанавливающая связь между параметрами системы. Например, давление газа – функция объема и температуры. Эта функция может быть и неоднозначной.
Для описания закрытой однокомпонентной системы могут быть выбраны параметры р, V, T. В этом случае уравнение состояния в общем виде может быть записано так:
F (р, V, T) = 0 (1.4)
Примеры уравнений состояния
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.