Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 41

Если раствор близок к идеальному, то для разности  можно написать

,                           (11.2)

где х₁ – молярная доля растворенного вещества.

Теперь можно поставить вопрос, а какое давление р следует приложить к раствору, чтобы химический потенциал растворителя в растворе стал бы равен химическому потенциалу чистого растворителя? Изменение μ под влиянием давления определяется в соответствии с (5.39) величиной

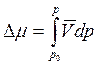, где  - парциальный молярный объем растворителя. Считая, что  не зависит от р, получаем

,                                   (11.3)

где π – осмотическое давление, равное

.

Приравнивая выражения (11.2) и (11.3), находим

или

,                                               (11.4)

где С – концентрация растворенного вещества. Осмотическое давление, как это следует из последней формулы, численно равно тому давлению, которое производил бы идеальный газ, взятый в концентрации С растворенного вещества.

Измерение осмотического давления можно произвести с помощью полунепроницаемых мембран, пропускающих только растворитель. В этом случае растворитель диффундирует сквозь мембрану в раствор до тех пор, пока давление жидкости в сосуде с раствором не скомпенсирует разность химических потенциалов.

Следует отметить, что формула (11.3) не очень точна. Лучшие результаты дает другая формула. Учитывая выражение (11.1), для химического потенциала растворителя в растворе можно записать

.                                                 (11.5)

Если давление р таково, что , то из уравнения (11.5) получим

.                                                     (11.6)

Величину а можно рассчитать, если известно давление пара растворителя над раствором. Так как в соответствии с (9.2) 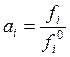, а в случае идеальной газовой фазы 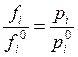, тогда

,                                               (11.7)

где р – давление паров растворителя над раствором, а р⁰ – давление над чистым растворителем. Формула (11.7) гораздо точнее описывает данные по осмотическому давлению. Таким образом, величина осмотического давления прямо связана с величиной активности растворителя.

12. адсорбция

Любая поверхностьспособна захватить (адсорбировать) молекулы из газовой или жидкой фазы. Адсорбцией называют явление образования поверхностного слоя с повышенной концентрацией газа или растворенного вещества на границе раздела с твердым телом или иной конденсированной фазой. Твердое тело при этом называют адсорбентом, а адсорбируемое вещество – адсорбатом. Явление удаления адсорбированного вещества с поверхности называют десорбцией.

Различают физическую адсорбцию, происходящую за счет дисперсионных (ван-дер-ваальсовских) взаимодействий молекул адсорбата с адсорбентом, образования водородных связей и т.п., и химическую адсорбцию (хемосорбцию), происходящую за счет образования химических связей между адсорбатом и адсорбентом. Для физической адсорбции характерны величины теплоты адсорбции ~ 2-5 кДж/моль, для химической адсорбции значения теплот обычно превышают 10 кДж/моль. Химическая адсорбция может сопровождаться диссоциацией молекул адсорбата и другими его химическими превращениями.

Специально приготовленные адсорбенты (например, силикагели, оксиды алюминия, активированные угли) могут иметь огромную удельную поверхность, измеряемую сотнями и даже тысячами м² на грамм адсорбента.

12.1. Изотерма адсорбции Генри

В простейшем случае равновесие между молекулами в газе (М) и молекулами на поверхности (М_п) можно записать как химическую реакцию:

М = М_п.

Константа равновесия записывается обычным образом:

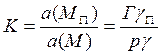, где а(М_п) – активность поверхностных молекул; а(М) – активность (летучесть) газофазных молекул; Г – концентрация адсорбированных молекул; р и γ – давление и коэффициент летучести молекул, выраженный в единицах моль/м² или (моль/см²); γ_п – коэффициент активности поверхностных молекул, в газовой фазе.

Если адсорбированные молекулы заполняют малую долю поверхности, то можно считать γ_п ≈ 1. Если давления невелики, то можно положить: γ ≈ 1. Тогда для величины Г получим