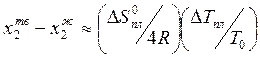. (10.25)
Это соотношение
можно использовать для экспериментальной проверки, насколько система (раствор)
близок к идеальной: экспериментально измеряется 
и
сравнивается с расчетом по (10.25).
Из (10.25)
видно, что ширина пропорциональна энтропии
плавления и разности температур плавления чистых веществ.
10.5. Фазовые диаграммы сложных видов
Пример,
рассмотренный на рисунке 10.5, соответствует достаточно простой фазовой
диаграмме. Это связано с тем, что кривые 
и 
с увеличением температуры остаются
простыми: имеют по одному экстремуму, вогнуты в одну сторону, пересекаются при
любой T не более чем в одной точке и т.д.
В более сложных
случаях кривые и с
изменением температуры могут деформироваться и пересекаться произвольным
образом. В этом случае фазовые диаграммы могут иметь весьма сложный вид. Число
фаз может быть максимальным. Могут существовать такие условия, при которых
одновременно могут существовать и жидкая фаза и несколько твердых одновременно.
Линии солидуса и ликвидуса могут иметь максимумы или минимумы.
Вид кривых 
может быть таким, что можно провести общую
касательную к двум точкам 
и одной 
одновременно (рис.10.6, а).
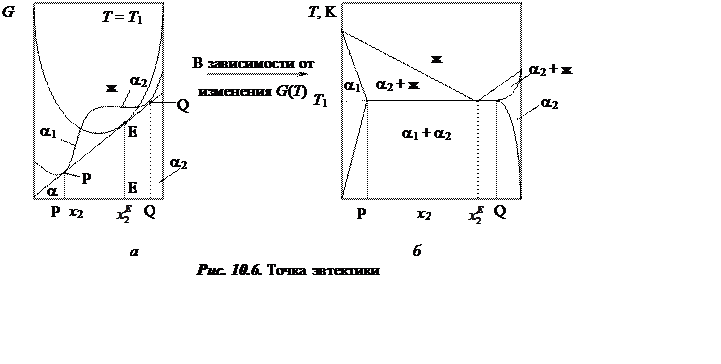
На рисунке 10.6
это точки P, Е, Q.
Точка Е соответствует условиям одновременного существования жидкой фазы, 
и 
. Такая точка называется точкой эвтектики,
а соответствующая температура - эвтектической. Это наиболее низкая температура,
при которой сплав 1 - 2 еще полностью или частично жидкий.
Состав 
- эвтектический состав.
Эвтектическая
точка характеризуется тем, что существует касательная, общая к кривым и двум кривым 
и 
, соответствующим двум твердым фазам. Причем
точка касания к лежит между точками касания
(равновесия) твердых растворов.
Перетектические
точки. Подобная ситуация может возникнуть и в другом случае (рис. 10.7),
при котором также возможно провести касательную к трем точкам , и , но точка касания (равновесия) для
жидкости не лежит между точками касания (равновесия) для твердых растворов.
Такая точка называется перетектической.
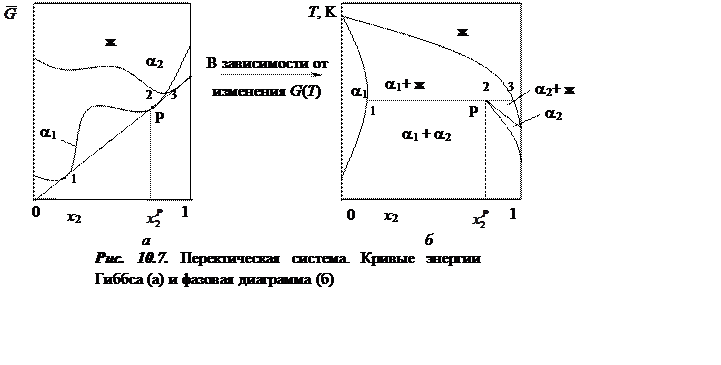
Если вместо
жидкой фазы в подобной ситуации выступает какая-то другая твердая фаза 
, то точку Р называют перетектоидной.
10.6. Расчет фазовых диаграмм
Расчет фазовых диаграмм сводится к расчету фазовых границ и равновесия между двумя фазами.
При равновесной
температуре Т равновесные составы 
и 
двух фаз aи b выражаются уравнениями
(8.7). Учитывая, что
, 
, (, Т, р ) 
, где g - коэффициент активности, уравнения (8.7) можно переписать в
виде:
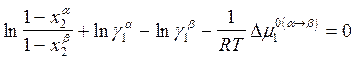, (10.26)
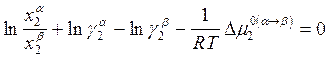, (10.27)
где 
-
разность значений химического потенциала i в
двух структурах a и b при давлении р = 1атм
(стандартное состояние по Раулю: р = 1атм, 
).
Логарифмический
коэффициент активности 
обычно можно выразить через молярные
доли x2 полиномами.
В этом случае
система уравнений (10.26 - 10.27) может быть решена относительно 
и 
. Обычно
решения находят численными методами, основанными на технике итераций, и другими
методами.
Иногда возникает необходимость по известным экспериментально определенным фазовым диаграммам определить термодинамические параметры (свойства). Эта задача решается как обратная к предыдущей. Методы решения применяются разные в зависимости от сложности системы.
11. осмотическое давление.
Явление осмоса заключается в диффузии молекул растворителя через полунепроницаемые мембраны, пропускающие только растворитель и разделяющие чистый растворитель и раствор (или растворы с различной концентрацией). Рассмотрим систему, состоящую из чистого растворителя и раствора, разделенных полунепроницаемой мембраной. Химический потенциал растворителя в растворе равен
, (11.1)
где 
- химический потенциал в состоянии
сравнения. Пусть состояние сравнения соответствует чистому веществу. Для
остальных величин отношение к чистому веществу показывается индексом «0». Из
(11.1)
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.