5.2. Экстенсивные свойства. Уравнение Гиббса-Дюгема
1) Функция f(x, y, z) называется однородной первой степени, если
![]() . (5.10)
. (5.10)
2) Для однородной функции первой степени f(x, y, z) справедливы соотношения
![]() , (5.11)
, (5.11)
![]() . (5.12)
. (5.12)
Здесь нижний индекс означает, что производная берется по этой переменной.
Определение. Экстенсивными свойствами системы являются функции, значения которых при прочих неизменных условиях пропорциональны числу молей в системе. К таким функциям относятся U, H, A, G, V, S. Математически функцию, характеризующую экстенсивное свойство, можно представить как однородную функцию первой степени, т.е.
При р и T = const
![]() , (5.13)
, (5.13)
![]() , (5.14)
, (5.14)
![]() . (5.15)
. (5.15)
Далее, если U = U(S, V, ni),то
U(λS, λV, λni) = λU(S, V, ni)(5.16)
При этом, если учесть, что [см. уравнение (5.5)]
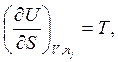
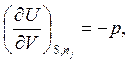
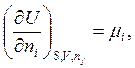
![]()
![]() (5.17)
(5.17)
можно получить, воспользовавшись свойствами (5.11) и (5.12), соответственно
![]() (5.18)
(5.18)
![]() . (5.19)
. (5.19)
Это уравнение носит название уравнения Гиббса - Дюгема. Его можно получить и непосредственно из (5.18). Действительно,
![]() . (5.20)
. (5.20)
С другой стороны, по определению и с учётом (5.17)
![]() . (5.21)
. (5.21)
Теперь, приравнивая правые части (5.20) и (5.21), можно получить уравнение Гиббса - Дюгема в виде (5.19).
Если T, р = const, то из (5.19) →
![]() (5.22)
(5.22)
Подставляя (5.18) в (3.19), (3.24), (3.29), можно получить также следующие аналогичные (5.18) соотношения:
![]() , (5.23)
, (5.23)
![]() , (5.24)
, (5.24)
![]() . (5.25)
. (5.25)
Последнее соотношение особенно важно. Оно широко используется при анализе многокомпонентных систем. Благодаря (5.23) - (5.25) в расчётах можно использовать парциальные свойства отдельных компонентов.
5.3. Основные соотношения для многокомпоненьных гомогенных систем
Частная
производная некоторой экстенсивной функции Y по
числу молей компонента i при постоянном числе
молей других компонентов j называется
парциальным мольным свойством и обозначается ![]() .
.
Пример
|
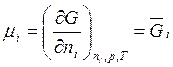 . (5.26)
. (5.26)
![]() - это
парциальная мольная энергия Гиббса, т.е.
- это
парциальная мольная энергия Гиббса, т.е.
![]()
![]() . (5.27)
. (5.27)
Аналогично
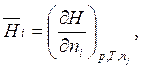 (5.28)
(5.28)
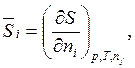 (5.29)
(5.29)
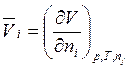 . (5.30)
. (5.30)
Частные мольные свойства могут рассматриваться при других постоянных переменных, например, Т, V = const.
Но если не оговаривается, далее всегда будут р, T = const при определении парциальных мольных свойств.
Если T = const, р = const, то экстенсивное свойство Y зависит только от ni и является однородной функцией этих переменных. В этом случае, согласно (5.11)
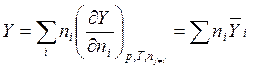 , (5.31)
, (5.31)
![]() . (5.32)
. (5.32)
С другой стороны,
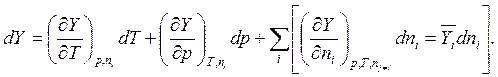 (5.33)
(5.33)
Из двух последних уравнений можно получить
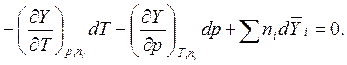 (5.34)
(5.34)
Эта формула – обобщённое уравнение Гиббса - Дюгема [см.(5.19)]. Или при постоянных Т и p
![]() . (5.35)
. (5.35)
Используя (5.34) для H, S, V можно получить уравнения в виде
![]()
![]() , (5.36)
, (5.36)
![]()
![]() (5.37)
(5.37)
![]()
![]() (5.38)
(5.38)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.