Химическая термодинамика: Конспект лекций (Законы термодинамики. Равновесия химических реакций. Графическое представление условия равновесия фаз), страница 30

Из (8.7) с учетом (5.41) и того, что для бинарной системы

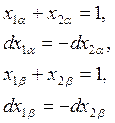
следует

,

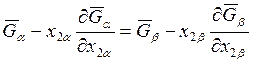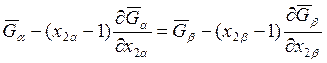.                                (8.9)

Вычитая из второго уравнения первое, получаем

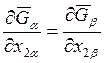.                                                     (8.10)

При выводе соотношения (8.10) предполагалось, что зависимости молярных энергий Гиббса  и  от состава определяются только величинами х_2a и х_2b соответственно. Если вместо х_2a и х_2b использовать х_1a и х_1b, то аналогичное уравнение будет иметь вид

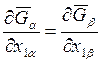.                                                     (8.11)

Уравнения (8.10) и (8.11) можно записать и без указания конкретного компонента в форме

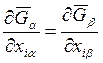,     (i = 1, 2).                                 (8.12)

Перейдем к рассмотрению дифференциальных уравнений (8.8). Для dμ_1α можно записать

.

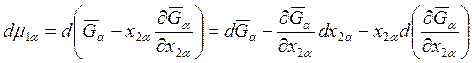Учитывая, что

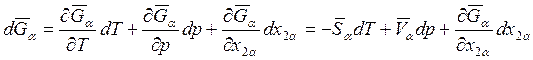, для dμ_1α получаем:

.

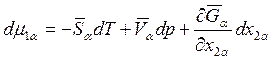Для dμ_1β можно записать аналогичное выражение

.

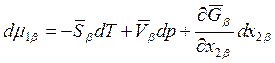Приравняв теперь dμ_1α и dμ_1β и учитывая соотношение (8.11), находим

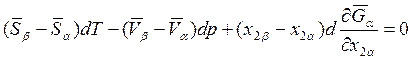                            (8.13)

или

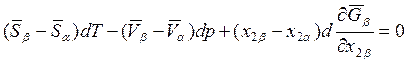.                            (8.14)

Аналогичные выражения можно записать, заменив х_2a и х_2b на х_1a и х_1b соответственно. Раскрывая выражение для 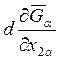, находим

.

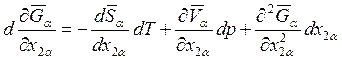Подставляя последнее выражение в (8.13), получаем

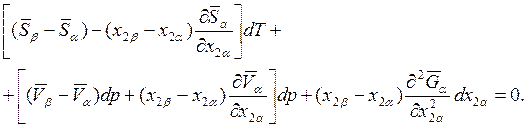                 (8.15)

Следует отметить, что в уравнении (8.15) величину  можно заменить на , х_ia на х_ib соответственно и записать его в следующей общей форме:

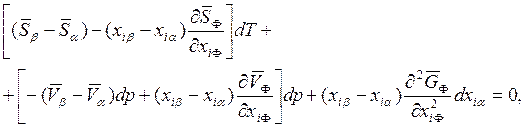                  (8.16)

где i = 1 или 2, а Φ = α или β. Уравнение (8.16) является наиболее общим уравнением, описывающим термодинамику двухфазных, двухкомпонентных систем. Оно носит название уравнение Ван дер Ваальса. Отметим, что в этом уравнении используются только молярные величины, относящиеся к одному молю фазы α или β.

На практике зачастую применяют несколько иные выражения для описания двухфазных, двухкомпонентных систем, в которых используются как молярные, так и парциальные молярные величины. Из уравнений (8.8)

получаем:

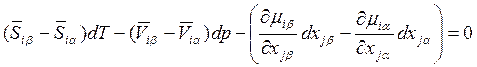,              (8.17)

где i, j = 1 или 2, i ≠ j. Так как в равновесии

, то для величины можно записать

, где .

Для определенности предположим, что в уравнении (8.17) j = 2. Тогда

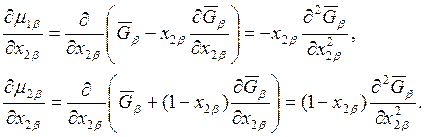                          (8.18)

Аналогично

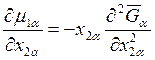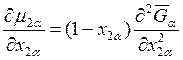,                .                      (8.19)

Подставляя уравнения (8.18) и (8.19) в выражение (8.17), получаем следующие два уравнения:

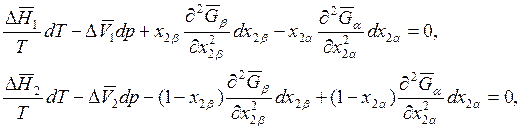                  (8.20)

где .

Уравнения (8.20) широко используются при описании двухфазных, двухкомпонентных систем. Из вывода уравнений (8.16) и (8.20) следует эквивалентность.

8.5. Уравнения фазового равновесия двухфазных двухкомпонентных систем

Под уравнением фазового равновесия будем понимать зависимость какого-либо одного термодинамического параметра от другого при постоянном значении третьего. Их удобно получать из общих уравнений (8.20). Уравнения (8.20) содержат четыре параметра, но из этих двух уравнений всегда можно исключить один термодинамический параметр и получить одно уравнение с тремя параметрами, из которых только две величины являются независимыми в полном соответствии с правилом фаз.

Рассмотрим сначала уравнения фазового равновесия при постоянстве состава одной из фаз, например α – фазы. Если х_2a = const и, следовательно, dх_2a = 0, то уравнения (8.20) будут иметь вид

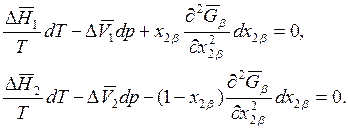
Выражая из первого уравнения 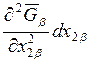 и подставляя во второе, для величины  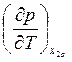находим

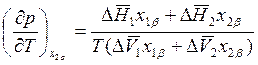.                                              (8.21)

В этом уравнении величины х_1b и х_2b могут зависеть от температуры наряду с  и . Выражение для величины 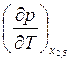 легко получается из (8.21) заменой индекса β на α. Уравнение (8.21) можно записать в более компактной форме:

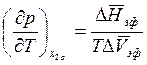,                                                        (8.22)

где

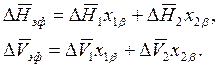
Для конкретности здесь и в дальнейшем условимся индекс «β» приписывать фазе с более высоким значением молярной энтропии. Например, если рассматривается равновесие между жидкостью и паром, то паровой фазе соотнесем индекс «β».

Аналогичным образом при х_2α = const находим

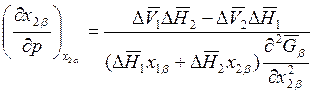;                                  (8.23)

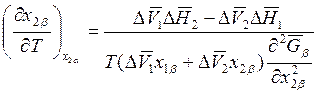.                                  (8.24)

Если T = const, то

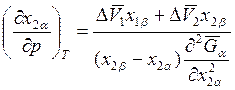;                                      (8.25)

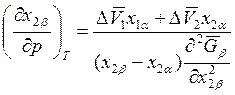;                                      (8.26)