Для решения вопроса о равновесном составе системы на практике используется два основных метода:
1) нахождение экстремума термодинамического потенциала системы;
2) использование уравнений закона действующих масс (константный метод).
Рассмотрим более подробно второй метод, основанный на использовании констант равновесия химических реакций и закона действующих масс.
Стадии расчета равновесного состава на основе использования закона действующих масс и констант равновесия химических реакций
1. При наличии достаточно большого числа элементов в системе число возможных индивидуальных веществ, образованных из этих элементов, может быть очень большим, поэтому первый вопрос, который необходимо решить, – это определение минимального набора веществ, которые следует учитывать в конечных продуктах.
2. Второй вопрос – как учитывать конденсированную фазу (необходим анализ веществ, которые могут образовать конденсированную фазу, состав конденсированной фазы и т.д.)
3. Набор конкретных реакций, приводящих систему к равновесному состоянию, не важен. Тем не менее, при анализе влияния состава системы на отклонение от равновесия необходимо выбрать некоторый минимальный набор независимых химических реакций, поскольку изменения содержания компонентов в реакции не являются независимыми, а определяются стехиометрическими уравнениями реакции.
Рассмотрим ситуацию, когда конденсированная фаза не образуется, а газ можно считать идеальным.
Известно, что само химическое равновесие не зависит от того, по какому термодинамическому пути оно достигалось (т. е. в результате осуществления каких реакций оно достигнуто). Для любой химической реакции (j) можно записать выражение для константы равновесия в виде закона действия масс
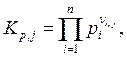(6.50)
где рi – парциальные давления компонента i; ni,j – матрица стехиометрических коэффициентов реакции (i- номер компонента, j – номер реакции, ni,j > 0 - для продуктов, ni,j < 0 - для исходных реагентов); Кр,j – константа равновесия соответствующей реакции (j).
Число возможных таких уравнений может быть достаточно произвольным для рассматриваемой системы, однако число независимых уравнений (нельзя допускать, чтобы какая-либо константа равновесия могла быть получена комбинацией других) будет равно числу возможных для данной системы независимых химических реакций.
Удобнее всего рассматривать образование веществ, которые в конечном итоге будут присутствовать при достижении химического равновесия, в предположении, что все они образуются непосредственно из элементов, т.е. в качестве независимых реакций взять реакции диссоциации рассматриваемых компонентов на атомы.
Этот прием удобен тем, что, во-первых, не требуется дополнительно анализировать, зависимы реакции или нет (все реакции автоматически получаются независимыми), и, во-вторых, тем, что он позволяет унифицировать справочные данные по константам реакций (требуются только константы диссоциации индивидуальных веществ, исключается необходимость исследовать все возможные реакции). Кроме того, эти константы широко представлены в справочниках и удобны для создания алгоритмов универсальных программ термодинамических расчётов равновесных составов.
Например, пусть необходимо определить константу равновесия реакции разложения этилена на ацетилен и водород:
C2H4 Û C2H2 + H2, (6.51)
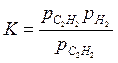(6.52)
Если известны константы диссоциации каждого из участвующих в реакции (6.51) веществ
C2H4 Û 2C + 4H, (6.53)
, (6.54)
C2H2 Û 2C + 2H, (6.55)
(6.56)
H2Û2H, (6.57)
(6.58)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.