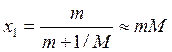 , где m
– моляльность, моль/кг; М – молекулярная масса молекул растворителя, выраженная
в кг/моль. Используя последнюю формулу, выражение (9.49) запишем следующим
образом:
, где m
– моляльность, моль/кг; М – молекулярная масса молекул растворителя, выраженная
в кг/моль. Используя последнюю формулу, выражение (9.49) запишем следующим
образом:
![]() , (9.50)
, (9.50)
где Е – эбулиоскопическая постоянная, равная
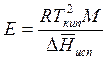 . (9.51)
. (9.51)
Метод эбулоскопии иногда используется для определения молекулярных весов, так как, зная Е и измеряя ΔТ, можно определить моляльность раствора, а зная вес растворенного вещества, можно легко рассчитать его молекулярный вес. Величина Е составляет 0,529 для воды и 6,09 для камфоры. Для более точного определения молекулярной массы желательно использовать вещества с возможно большими значениями величины Е.
Полезно получить формулу (9.49) из общего выражения (8.28). Так как в жидкой фазе растворен нелетучий компонент, то в газовой фазе будем иметь
![]() ,
, ![]() , (9.52)
, (9.52)
а для разности ![]() получим
получим
![]() . (9.53)
. (9.53)
Подставляя (9.43) в (8.28), приходим к той же формуле (9.49) для повышения температуры кипения.
9.7. Правила Вревского
Первое
правило Вревского гласит, что при повышении температуры смеси определенного
состава ее пар обогащается тем компонентом, который обладает большей парциальной
теплотой испарения. Это правило представляет собой простое следствие
уравнения (8.24). Действительно, для стабильных фаз всегда выполняется условие 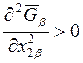 . Объемом жидкой фазы по сравнению с
объемом газовой фазы можно пренебречь и, считая газы идеальными, для
. Объемом жидкой фазы по сравнению с
объемом газовой фазы можно пренебречь и, считая газы идеальными, для ![]() можно записать:
можно записать:
![]() . (9.54)
. (9.54)
Подставляя последнее выражение в (8.24), находим
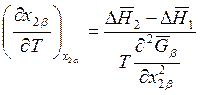 . (9.55)
. (9.55)
Если ![]() , то пар
будет обогащаться вторым компонентом и наоборот.
, то пар
будет обогащаться вторым компонентом и наоборот.
Второе правило Вревского гласит, что если на фазовых диаграммах давление – состав (температура – состав) имеется максимум (минимум), то при повышении температуры в азеотропе увеличивается молярная доля компонента с большей парциальной теплотой испарения; если на фазовых диаграммах давление – состав (температура – состав) имеется минимум (максимум), то при повышении температуры в азеотропе увеличивается молярная доля компонента с меньшей парциальной теплотой испарения. Напомним, что для азеотропа выполняется условие
![]() . (9.56)
. (9.56)
Для определенности предположим,
что α – жидкая фаза, а β – газовая. Выясним поведение величины ![]() (или
(или ![]() ) с
температурой в условиях азеотропа. Для этого рассмотрим величину
) с
температурой в условиях азеотропа. Для этого рассмотрим величину 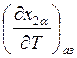 , где индекс «аз» означает «азеотроп». Если
из первого уравнения системы (8.20) выразить величину dp
и подставить во второе, то с учетом равенства (9.56) и
, где индекс «аз» означает «азеотроп». Если
из первого уравнения системы (8.20) выразить величину dp
и подставить во второе, то с учетом равенства (9.56) и
![]()
получаем
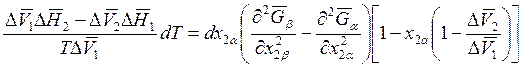 . (9.57)
. (9.57)
Считая газы идеальными и пренебрегая молярными объемами жидкостей, имеем
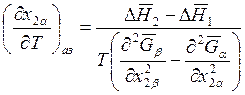 . (9.58)
. (9.58)
Из последнего уравнения видно,
что знак величины 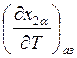 зависит от соотношения величин
зависит от соотношения величин ![]() и
и ![]() , с одной
стороны, и
, с одной
стороны, и 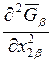 и
и 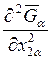 - с
другой. Рассмотрим соотношение между последними величинами с помощью уравнения
(8.27). Легко убедиться в том, что в случае идеальной паровой фазы уравнение
(8.27) будет иметь вид
- с
другой. Рассмотрим соотношение между последними величинами с помощью уравнения
(8.27). Легко убедиться в том, что в случае идеальной паровой фазы уравнение
(8.27) будет иметь вид
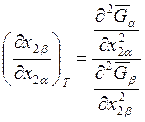 . (9.59)
. (9.59)
Это уравнение описывает
зависимость ![]() от
от ![]() .
Применительно к рассматриваемому случаю эти зависимости могут быть двух типов в
соответствии с рис. 9.1, е и 9.1, и. В случае «е» в точке
.
Применительно к рассматриваемому случаю эти зависимости могут быть двух типов в
соответствии с рис. 9.1, е и 9.1, и. В случае «е» в точке ![]() величина производной
величина производной 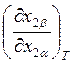 меньше единицы. Это означает, что при х2
= 0 величина производной
меньше единицы. Это означает, что при х2
= 0 величина производной 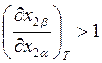 и, следовательно,
кривая пара вблизи х2 = 0 расположена правее кривой жидкости.
Это возможно только тогда, когда на кривой давление - состав имеется максимум
(см. рис. 9.1, г). Итак, в случае «е» азеотропный состав характеризуется
соотношением
и, следовательно,
кривая пара вблизи х2 = 0 расположена правее кривой жидкости.
Это возможно только тогда, когда на кривой давление - состав имеется максимум
(см. рис. 9.1, г). Итак, в случае «е» азеотропный состав характеризуется
соотношением 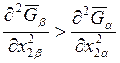 . Обратившись к уравнению (9.58),
видим, что величина
. Обратившись к уравнению (9.58),
видим, что величина 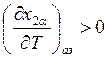 , если
, если ![]() .
Следовательно, с ростом температуры величина
.
Следовательно, с ростом температуры величина ![]() будет
расти и смещение азеотропа будет иметь вид, показанный на рис. 9.5, а.
Существование минимума на кривых давление – состав приведет нас к противоположному
выводу (рис. 9.5, б).
будет
расти и смещение азеотропа будет иметь вид, показанный на рис. 9.5, а.
Существование минимума на кривых давление – состав приведет нас к противоположному
выводу (рис. 9.5, б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.