Для идеальных растворов (определение)
ai = xi (5.68)
Для реальных
ai = gi xi , (5.69)
gi – коэффициент активности gi (T, p, xj).
Понятия ai и gi – эквивалентны, введено две величины для удобства при проведении вычислений и измерений.
Энергия Гиббса в случае неидеальной системы на основе (5.25) и (5.64):
![]() (5.70)
(5.70)
С учетом выражения (5.70) уравнение Гиббса-Дюгема (5.22) при постоянных значениях Т и р выглядит следующим образом:
![]() (5.71)
(5.71)
Так как в случае идеальной системы
![]() ,
(5.72)
,
(5.72)
то уравнение Гиббса - Дюгема (5.71) в терминах коэффициента активности будет иметь вид
![]() (5.73)
(5.73)
6. РАВНОВЕСИЯ ХИМИЧЕСКИХ РЕАКЦИЙ
6.1. Случай равновесия одной химической реакции
Пусть имеем одну реакцию
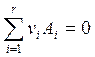 , (6.1)
, (6.1)
где ni – стехиометрический коэффициент (ni > 0 – продукты; ni < 0 – реагенты).
Очевидно,
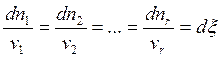 . (6.2)
. (6.2)
Условный параметр x вводится для удобства и называется химической переменной или координатой реакции. Введением x подчёркивается, что процесс химического превращения в случае одной реакции зависит лишь от одной переменной (любую величину dni можно выразить через x: dni = ni dx).
Изменение энергии Гиббса в зависимости от р, T,ni в соответствии с (5.8) или табл.5.1.
![]() .
.
Или
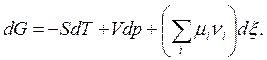 (6.3)
(6.3)
Если р, Т = const, то в качестве критерия равновесия i имеем:
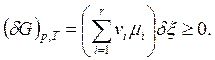 (6.4)
(6.4)
Так как знак ånimi постоянен, а dxможет быть как > 0, так и < 0, то (6.4) будет выполняться лишь в случае
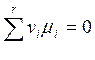 (6.5)
(6.5)
Это и есть условие равновесия химической реакции.
Из (6.3) при р, T= const ®

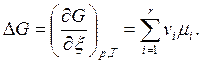 (6.6)
(6.6)
Следовательно, для случая равновесия имеем
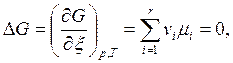 (6.7)
(6.7)
т.е. условие равновесия химической реакции при постоянных р и Т – это условие экстремума функции G(x) (рис. 6.1).
Если имеет место состояние, отличное от равновесия, то движение по левой ветви соответствует случаю dx > 0 – количество продуктов увеличивается – преобладает прямая реакция.
Движения по правой ветви к точке равновесия dx < 0 – количество продуктов убывает – преобладает обратная реакция.
Если mi выразить через летучести fi , связанные с парциальным давлением рi, или через активности ai, связанные с концентрациями веществ xi,то условие равновесия можно использовать для нахождения равновесных парциальных давлений или концентраций.
При этом условие химического равновесия выражается в виде известного закона действия масс.
В общем случае для газов
![]() (6.8)
(6.8)
где fi – летучесть i-го компонента в смеси; mi0 – химический потенциал i-го компонента в стандартном состоянии (когда fi=1), mi0= mi0(T).
В общем случае для конденсированных веществ (жидкостей или твёрдых)
mi = mi* + RT ln ai , (6.9)
где ai – активность i-го компонента в растворе, mi* – химический потенциал в состоянии сравнения (когда ai = 1, т.е. для чистого компонента в том же фазовом состоянии).
Мольные значения G в стандартных условиях обозначают через G0.
Удобно ввести величины DG0 и DG [см.(6.6)].
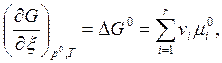 (6.10)
(6.10)
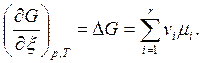 (6.11)
(6.11)
Как это видно, изменение энергии Гиббса в результате химической реакции зависит от выбора стехиометрических коэффициентов.
Подставляя в (6.5) mi из (6.8), условие равновесия можно получить в виде
![]() , (6.12)
, (6.12)
или
![]() , (6.13)
, (6.13)
или
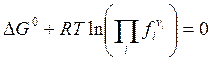 , (6.14)
, (6.14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.