Аналогичным образом можно рассмотреть и остальные случаи, относящиеся ко второму правилу Вревского.
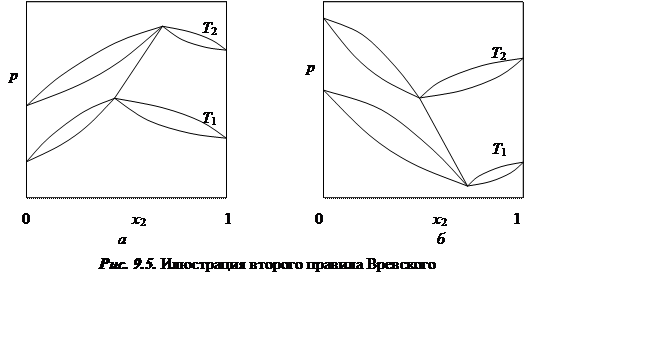
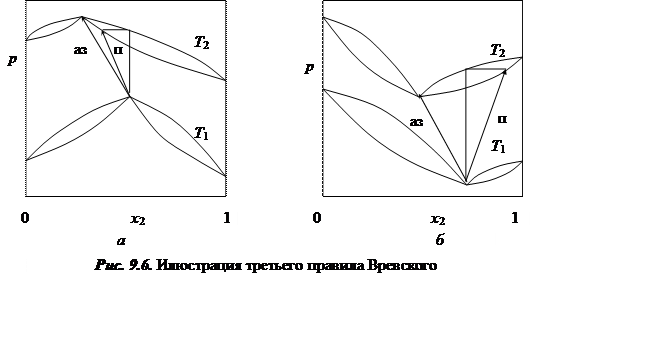
Третье правило Вревского гласит, что если на фазовых диаграммах давление пара – состав (температура – состав) имеется максимум (минимум), то при изменении температуры азеотропного раствора состав пара и состав азеотропа меняются в одном направлении; если на фазовых диаграммах давление пара – состав (темепратура – состав) имеется минимум (максимум), то при изменении температуры азеотропного раствора состав пара и состав азеотропа меняются в противоположном направлении (рис. 9.6).
Для анализа этих утверждений
рассмотрим величины 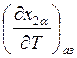 - выражение (9.58) и
- выражение (9.58) и 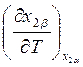 - выражение (8.24). Поделив их друг на
друга, найдем
- выражение (8.24). Поделив их друг на
друга, найдем
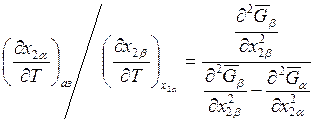 . (9.60)
. (9.60)
Знак выражения (9.60) определяется знаком знаменателя. Ранее было показано, что если на кривой давление пара – состав имеется максимум, то величина знаменателя положительна и, следовательно, составы пара и азеотропа будут изменяться в одном направлении. Для кривых с минимумом это изменение будет носить противоположный характер.
Необходимо отметить, что в условиях, близких к критическим, правила Вревского могут нарушаться.
10. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ УСЛОВИЯ РАВНОВЕСИЯ ФАЗ
10.1. Метод касательных для бинарной системы
Пусть имеется бинарная система, Y – любое термодинамическое свойство этой системы. х1 и х2 – молярные доли вещества 1 и вещества 2
![]() .
.
Рассмотрим
график ![]() .
.
Касательная к
точке М отсекает (рис. 10.1) на оси х1 = 1 отрезок ![]() а на оси х2 = 1 отрезок
а на оси х2 = 1 отрезок ![]() где
где 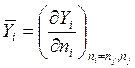 .
.
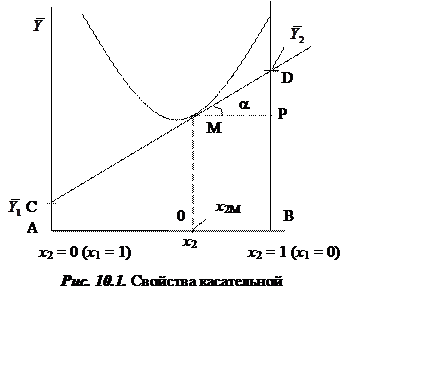
Доказательство:
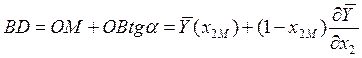 . (10.1)
. (10.1)
Если ![]() , то
, то
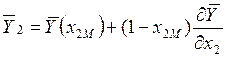 . (10.2)
. (10.2)
Аналогично, если АС =![]() , то
, то
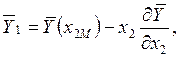
где x2М - значение х2, соответствующее точке М.
Докажем (10.2):
![]() (10.3)
(10.3)
для идеальной системы (по определению идеальной системы).
Дифференцирование (10.3) дает
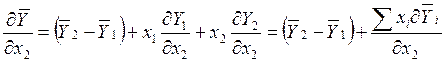 , (10.4)
, (10.4)
так как в соответствии с уравнением Гиббса – Дюгема (при р, Т = const),
![]() , то из (10.4)
, то из (10.4)
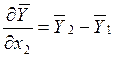 . (10.5)
. (10.5)
Выражая ![]() из (10.3) и подставляя в (10.5),
получим
из (10.3) и подставляя в (10.5),
получим
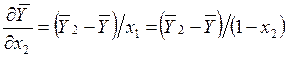 , (10.6)
, (10.6)
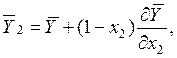 (10.7)
(10.7)
Если ![]() , что означает
, что означает
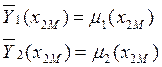 , (10.8)
, (10.8)
то, основываясь
на свойствах касательной, можно утверждать, что касательная к кривой ![]() в точке М отсекает:
в точке М отсекает:
на оси ![]()
![]() отрезок, равный
отрезок, равный ![]() , на оси
, на оси ![]()
![]() отрезок, равный
отрезок, равный ![]() .
.
Условием равновесия фаз a и b являются уравнения (8.7) и (8.8). Относительно х2a и х2b эти уравнения можно решить графически, используя свойство касательных.
Действительно,
если к кривым ![]() и
и ![]() провести
общую касательную (рис.10.2), то на оси
провести
общую касательную (рис.10.2), то на оси ![]() отсекутся
значения
отсекутся
значения ![]() , а на оси
, а на оси ![]() -
значения
-
значения ![]() . Здесь мольные доли определяются исходя из
того, что
. Здесь мольные доли определяются исходя из
того, что ![]()
![]()
![]()
![]() .
.
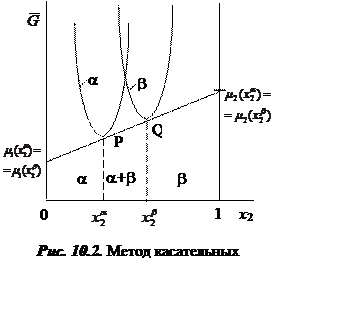
Пусть ![]() - общая мольная доля вещества «2» в
системе;
- общая мольная доля вещества «2» в
системе;
![]() - мольная доля фазы a в смеси;
- мольная доля фазы a в смеси;
![]() - число молей в фазе a;
- число молей в фазе a;
![]() - мольные энергии Гиббса системы, фазы a и фазы b
- мольные энергии Гиббса системы, фазы a и фазы b
В этом случае
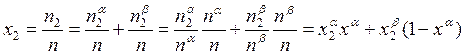 , (10.9)
, (10.9)
![]() . (10.10)
. (10.10)
Из (10.9)
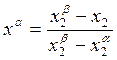 ;
; 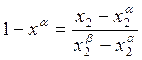 . (10.11)
. (10.11)
Из рисунка и представленных соотношений следует, что:
1. ![]() при
при ![]() , т.е. в
системе присутствует только фаза a;
, т.е. в
системе присутствует только фаза a; ![]() ;
;
2. ![]() при
при ![]() , т.е.
система состоит из двух фаз a и b фиксированного состава, определяемых из
(8.7), (8.8) аналитически, численно или графически (см. рис. 10.1). Доля каждой
из фаз в системе определяется уравнениями (10.11). Энергия Гиббса системы
представлена на рисунке отрезком PQ в этом интервале
, т.е.
система состоит из двух фаз a и b фиксированного состава, определяемых из
(8.7), (8.8) аналитически, численно или графически (см. рис. 10.1). Доля каждой
из фаз в системе определяется уравнениями (10.11). Энергия Гиббса системы
представлена на рисунке отрезком PQ в этом интервале ![]() ;
;
3. при ![]() присутствует только фаза b,
присутствует только фаза b, ![]() .
.
10.2 Фазовые диаграммы бинарных систем
Когда р = const, а Т = var, можно построить диаграммы, связывающие температуру и состав. Диаграммы такого типа называют фазовыми. Фазовая диаграмма с сечением, соответствующим рисунку 10.2, показана на рис. 10.3.

10.3 Три фазы в бинарной системе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.