1) зная, что S = 0, при Т = 0 из (2.5) и (3.27) можно получить для изобарического и изохорического процессов соответственно
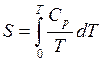 , (4.1)
, (4.1)
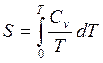 ; (4.2)
; (4.2)
2) из третьего закона (∂S/∂р)T=0 = 0, т.к. (∂S)T=0 =0, но из уравнения Максвелла
(∂S/∂p)T = - (∂V/∂T)p = - αV → (α)T=0 = 0 (4.3)
(это же следует и из экспериментов);
3) аналогично
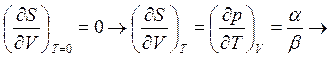
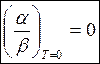 , (4.4)
, (4.4)
где 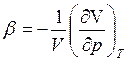 коэффициент
сжатия.
коэффициент
сжатия.
Отметим, что соотношение типа (∂р/∂T)V = α/β могут быть получены на основе использования уравнений Максвелла (см. табл. 3.1):
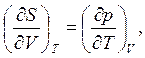 (4.5)
(4.5)
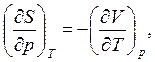 (4.6)
(4.6)
или
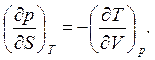 (4.7)
(4.7)
Комбинируя (4.5) и (4.7), получаем
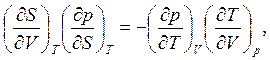 (4.8)
(4.8)
откуда
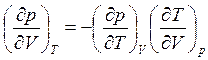 (4.9)
(4.9)
Так
как по определению 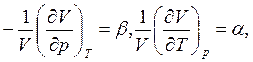 то
то
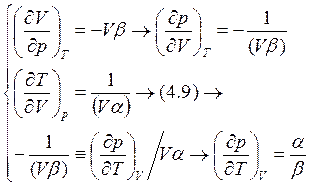 |
(4.10)
(4.11)
(4.12)
a- коэффициент объемного термического расширения,
b - коэффициент сжатия.
4.4. Изменение энтальпии и энтропии (пример)
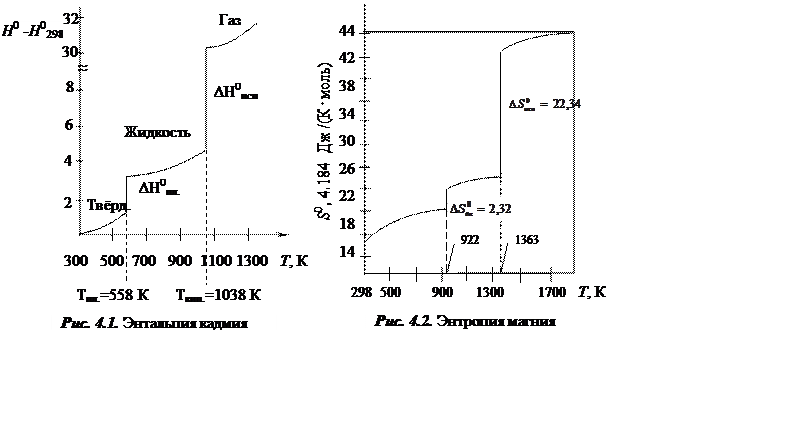
На рис. 4.1. и 4.2. показаны зависимости энтальпии кадмия и энтропии магния соответственно. Характерными для этих зависимостей являются наклоны кривых, которые характеризуются производными
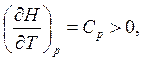
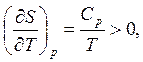 т.е.
т.е. ![]() .
.
Зависимость ΔН0 и ΔS0от температуры и для фазовых переходов имеется в таблицах термодинамических свойств веществ. (∂S/∂T)p – мала, часто пренебрегают температурной зависимостью для S.
4.5. Энтропия химических реакций
Для реакции
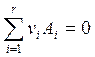 (4.13)
(4.13)
Изменение энтропии в результате реакции
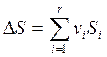 , (4.14)
, (4.14)
где Si – мольные энтропии компонентов Аi.
Определение энтропий образования (Sf) вещества аналогично изложенному в п. 2.5. для энтальпии. Для изолированной системы ΔS ≥ 0, но при обмене энергией и работой с внешней средой ∆S может иметь любой знак, так в реакциях:
Zr + O2 (газ) = ZrO2 (тв.) - ∆S10000 = - 184,34 Дж/(К·моль) (из таблиц)
C + O2 (газ) = CO2 (газ) - ∆S10000 = 1,25 Дж/(К·моль) (из таблиц)
C + CO2 (газ) = 2CO (газ) - ∆S10000 = 175,14 Дж/(К·моль) (из таблиц)
C (тв.) + SiO2 (тв.) = SiO (газ) + СO(газ) - ∆S10000 = 389,99 Дж/(К·моль) (из таблиц)
5. многокомпонентные системы
Рассмотрим гомогенную многокомпонентную систему. Эта открытая система состоит из одной фазы, но из многих компонентов.
5.1. Химический потенциал
Для описания открытой системы, кроме обычных переменных, например, (p, Т), необходимо ввести дополнительные, характеризующие её размер и состав. Открытые системы характеризуются обычно постоянством объёма, поэтому для их описания удобно выбрать энтропию S, объём V и число молей ni её компонентов. При этом внутренняя энергия системы
![]() . (5.1)
. (5.1)
Очевидно, полный дифференциал в этих переменных
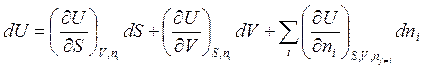 . (5.2)
. (5.2)
Первые частные производные (ni = const) аналогичны таковым для случая закрытых систем, следовательно, (см. табл. 3.1) (∂U/∂S)V = Tи (∂U/∂V)S = - р. Отсюда →
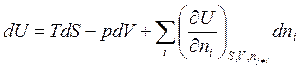 (5.3)
(5.3)
Величину
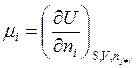 (5.4)
(5.4)
называют химическим потенциалом компонента i.
C учётом (5.4), (5.3) можно переписать в следующем виде:
![]() . (5.5)
. (5.5)
Аналогично (см.табл.3.1) можно записать уравнения для энтальпии (Н), энергии Гельмгольца (А) и энергии Гиббса (G).
![]() , (5.6)
, (5.6)
![]() , (5.7)
, (5.7)
![]() . (5.8)
. (5.8)
При этом можно получить [зная dU в виде (3.13)], что химический потенциал
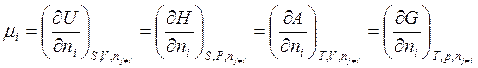 . (5.9)
. (5.9)
В частности, из (5.9) следует, что μi – это удельное изменение полной энергии Гиббса системы при добавлении к ней бесконечно малого количества компонента i при постоянной температуре и давлении (без изменения числа молей других компонентов j).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.