Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы

ЧАСТЬ 1

ОСНОВЫ ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

ГЛАВА 1

ИСПОЛЬЗУЕМЫЙ МАТЕМАТИЧЕСКИЙ АППАРАТ

В теории электромагнитного поля используются: векторная алгебра, векторный анализ, функции комплексной переменной, дифференциальные уравнения в частных производных гиперболического типа, решения которых приводят к тригонометрическим функциям, функциям Бесселя и другим специальным функциям.

1.1. Векторы и действия над ними

Вектором называется величина, характеризующаяся, помимо измеряющего ее в определенных единицах меры числа, еще своим направлением в пространстве. Численное значение вектора называется величиной, модулем или длиной вектора. Для численного задания вектора нужно указать три числа - три координаты вектора.

Любой вектор можно представить в виде разложения

A = x₀ A_x + y₀ A_y + z₀ A_z                                        (1.1)

где A_x , A_y , A_z  - проекции вектора на оси координат, x₀ , y₀ , z₀ - орты (единичные векторы) определяющие положение системы координат в пространстве.

Сложение векторов сводится к сложению их компонент

A + B = x₀ (A_x + B_x) + y₀ (A_y + B_y) + z₀ (A_z + B_z)            (1.2)

Сложение векторов подчиняется правилу геометрического сложения, как показано на рис. 1.1.

Из выражения (1.2) следует

C = A + B = C C₀ = x₀ (A_x + B_x) + y₀ (A_y + B_y) + z₀ (A_z + B_z)             (1.3)

где  ,

C₀ = cos (x₀ , C) x₀ + cos (y₀ , C) y₀ + cos (z₀, C) z₀ ,

.

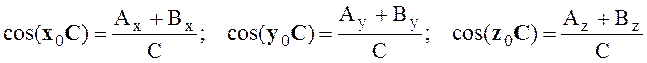Векторы А и В называются слагаемыми вектора, вектор С - геометрической суммой или результирующим вектором.

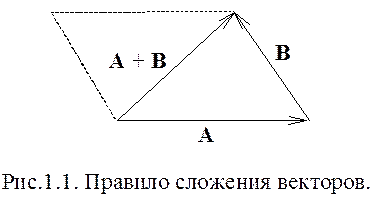
Действием, обратным геометрическому сложению, является вычитание. Чтобы вычесть из вектора А вектор В, надо прибавить к вектору А вектор В с обратным знаком - противоположный по направлению вектору В, как  показано на рис. 1.2.

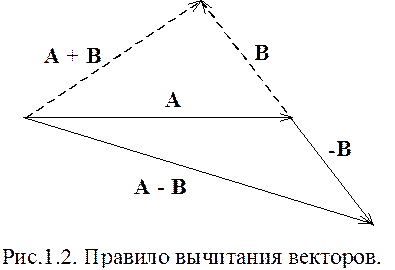
Помимо геометрического вычитания вектора возможно также геометрическое разложение, состоящее в том, что данный вектор заменяют суммой нескольких векторов. Геометрически эта операция сводится к построению ломаной линии, имеющей данный вектор замыкающей стороной, как показано на рис. 1.3.

Чтобы сделать задачу разложения векторов определенной, требуется наложить на геометрические слагаемые ряд условий.

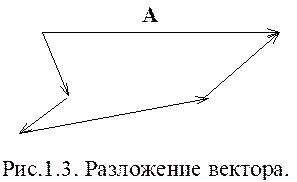
Чтобы сделать задачу разложения векторов определенной, требуется наложить на геометрические слагаемые ряд условий.

Умножение вектора на скаляр означает изменение длины вектора во столько раз, какое значение имеет скаляр, и без изменения направления вектора

m A = m A a₀                                                          (1.4)

где a₀ - единичный вектор, показывающий направление вектора А.

Параллельные между собой векторы называются также коллинеарными.

Если векторы А и В не коллинеарны, то вектор

C = m A + n B                                                         (1.5)

параллелен плоскости, определяемой векторами А и В. В этом случае говорят, что векторы А, В и С компланарны, то есть параллельны одной плоскости.

Обратно, всякий вектор С компланарный двум неколлинеарным векторам А и В, может быть представлен формулой (1.5).

Если три вектора А, В и С не компланарны, то всякий вектор D может быть представлен в форме

D = m A + n B + p C                                                         (1.6)

Скалярным или внутренним произведением двух векторов А и В называется произведение длин обоих векторов, умноженное на косинус угла между ними.

(A, B) = A × B = A B cos (A, B)                                        (1.7)

Важнейшие свойства скалярного произведения:

A B = B A; A B = 0, если A = 0 или B = 0, или A ^ B;

A B = ±  A B, если A и B коллинеарны, в частности A * A = A²

 

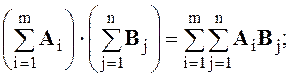
Векторным или внешним произведением двух векторов А и В называется вектор, по величине равный площади параллелограмма, построенного на векторах А и В, перпендикулярный плоскости, образованной этими векторами и направленный в такую сторону, чтобы вращение от А к В на кратчайшем пути вокруг полученного вектора происходило в ту же сторону, как вращение от оси х к оси у вокруг оси z (рис. 1.4.)

[A, B] = A ´ B = u₀ A B sin (A, B) ,                                 (1.8)

где u₀  - орт, направленный по нормали к плоскости векторов А и В, причем так, чтобы кратчайшее угловое расстояние между их направлениями, обозначенное на рис.1.4 стрелкой, соответствовало движению от А к В по часовой стрелке, если смотреть вдоль u₀ .

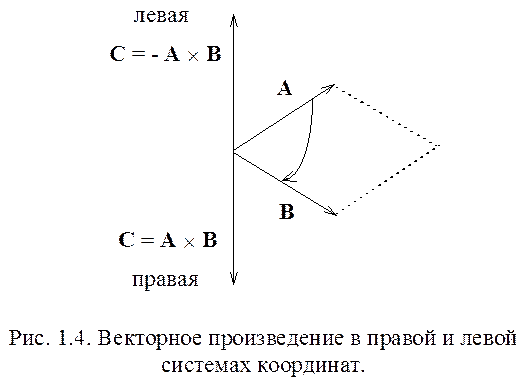
Важнейшие свойства векторного произведения

B ´ A = - A ´ B; A ´ B = 0, если A = 0 или B = 0, или A ïï B; A ´ A = 0;

 

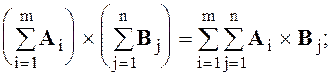
Векторное произведение можно записать в декартовой системе координат в виде определителя

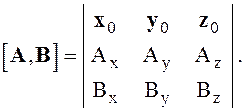                                                 (1.9)

Векторно-скалярное или смешанное произведение имеет вид

A [B, C]

Сначала вектор В умножается векторно на вектор С, а затем полученный результат умножается скалярно на вектор А.

Векторно-скалярное произведение равно объему параллелепипеда, построенного на векторах А, В и С как показано на рис. 1.5

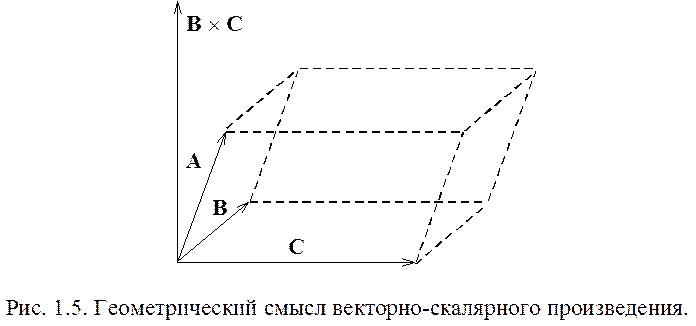
Свойства векторно-скалярного произведения:

При циклической перестановке векторов (замена А на В, В на С, С на А) векторно-скалярное произведение не меняется

A [B, C] = B [C, A] = C [A, B] ;                                       (1.10)