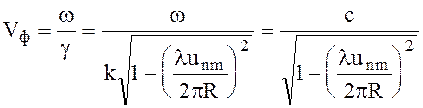Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 37

                    (6.100)

Групповая скорость

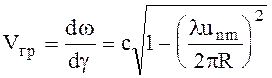                                   (6.101)

Из всех Е-волн в круглом волноводе наиболее часто используется волна Е₀₁ (n = 0, m = 1). Выражения составляющих поля волны Е₀₁ согласно (6.93) принимают вид

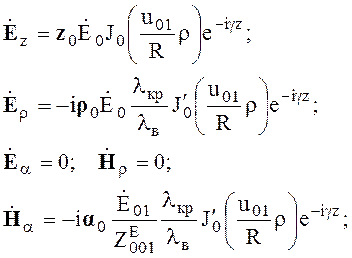                               (6.102)

Структура волны Е₀₁ показана на рис. 6.15. Из рис. 6.15. видно, что волна имеет осевую симметрию. Благодаря наличию осевой симметрии составляющих электромагнитного поля эта волна применяется во вращающихся сочленениях, которые предназначены для передачи электромагнитной энергии от неподвижного волновода к вращающейся антенне.

Все параметры волны Е₀₁ описываются выражениями (6.94 ... 6.101) при условии (n = 0, m = 1).

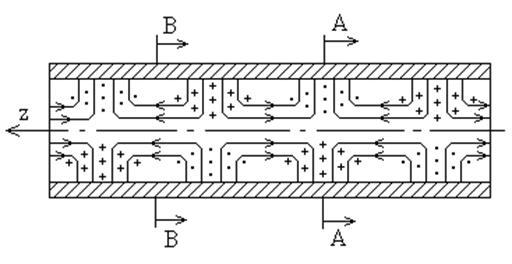
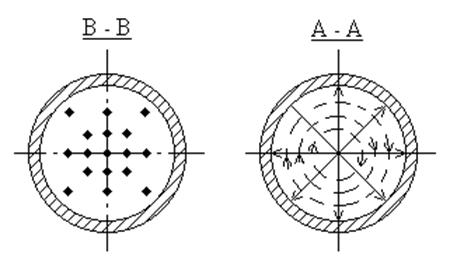
Рис. 6.15. Структура волны E₀₁ в круглом волноводе.

Н-волны

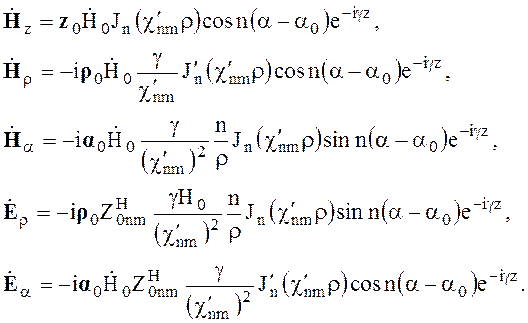  (6.103)

Здесь для определения  используются граничные условия второй краевой задачи

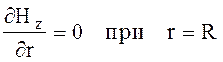                                 (6.104)

или  и таблица 6.2 значений .

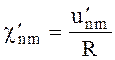                                         (6.105)

Характеристическое сопротивление

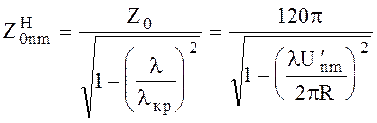                           (6.106)

Остальные параметры определяются выражениями (6.94), (6.95), (6.97...6.101) при замене в них  на .

Из всех Н-волн в круглом волноводе наименьшую критическую частоту имеет волна Н₁₁ (n = 1, m = 1). Выражения для составляющих поля волны Н₁₁ согласно (6.103) принимают вид

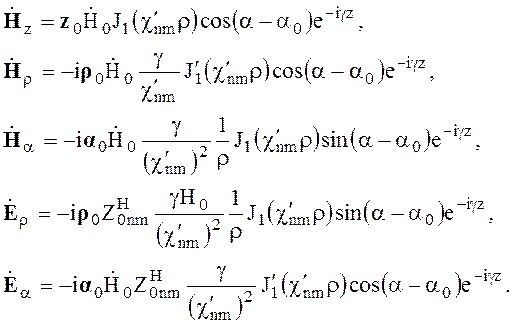               (6.107)

Для волны H₁₁

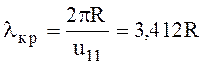                                    (6.108)

Структура волны Н₁₁ показана на рис. 6.16. Из рисунка видно, что волна по своей структуре похожа на волну Н₁₀ в прямоугольном волноводе.

Волна Н₁₁ имеет существенный недостаток. При распространении по волноводу наличие неоднородностей может привести к повороту плоскости поляризации волны, что приводит к нарушению режима работы линии.

Кроме волны Н₁₁ также широко применяется волна Н₀₁ (n=0, m=1). Выражение (6.103) для волны Н₀₁ принимает вид

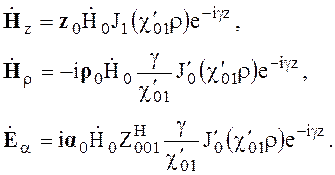                                  (6.109)

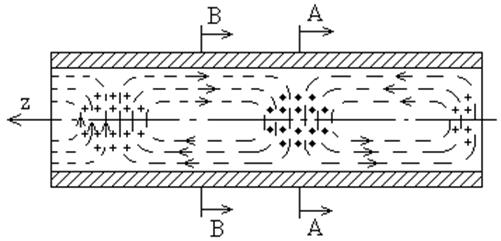
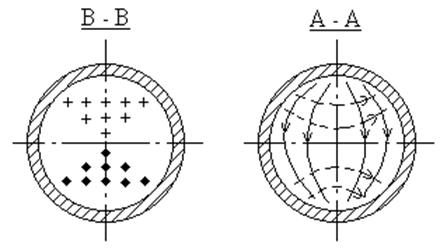
Рис. 6.16. Структура волны Н₁₁ в круглом волноводе.

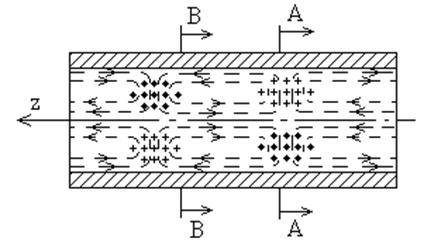
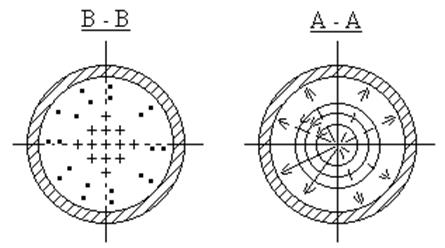
Рис. 6.17. Структура волны Н₀₁ в круглом волноводе.

Для волны Н₀₁

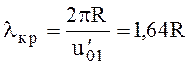                                      (6.110)

Структура волны Н₀₁ показана на рис. 6.17.

Параметры волны Н₀₁ определяются теми же выражениями, что и параметры волны Н₁₁, при замене в них u'₁₁ на u'₀₁.

Передаваемая мощность для Е - волн

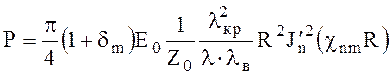                         (6.111)

Передаваемая мощность для Н - волн

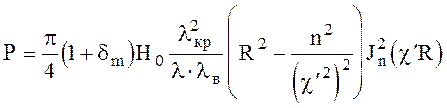                (6.112)

Здесь d_m = 1 при n = 0 и d_m = 0 при n ³ 1.

Потери в стенках круглого волновода для Е - волн

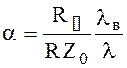                                                 (6.113)

Потери для Н-волн

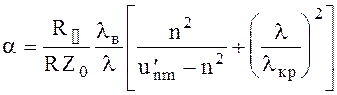                                  (6.114)

Из выражения (6.113) и (6.114) видно, что потери будут минимальными для волн типа Н_0m

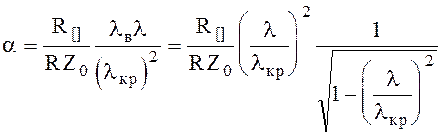                          (6.115)

Для волн типа Н_om видно из (6.115), что с увеличение частоты (уменьшением длины волны) потери уменьшаются, в то время как у всех других типов волн потери с повышением частоты увеличиваются.

Диаграмма типов волн для круглого волновода имеет вид, показанный на рис. 6.18.

6.6. Волны в коаксиальной линии передачи

Коаксиальная линия передачи показана на рис. 6.19.

Коаксиальная линия передачи в отличии от ранее рассмотренных волноводов способна передавать ТЕМ-волны, такие волны, у которых отсутствуют продольные составляющие векторов Е и Н, то есть  =  = 0.

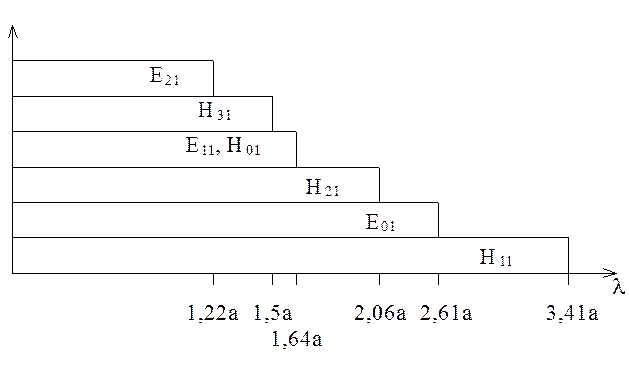
Рис. 6.18. Диаграмма типов волн для круглого волновода.

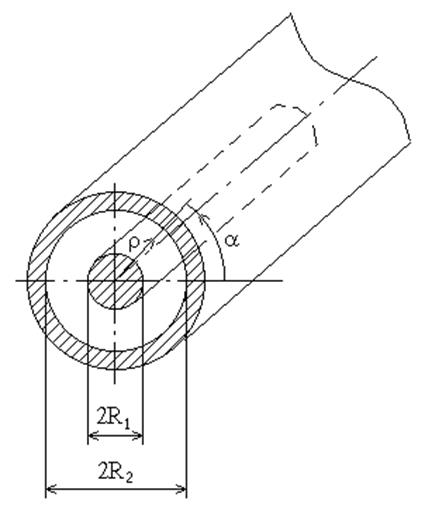
Рис. 6.19. Коаксиальная линия передачи.

Из уравнений (6.92) видно что при  должны выполняться равенства

                         (6.116)

Для того, чтобы поперечные составляющие не были равны нулю, требуется выполнение условия

                                           (6.117)

Отсюда ,

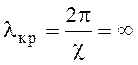                                               (6.118)

Следовательно, f_кр = 0.

Можно сделать вывод, что в тех линиях передачи, где существуют ТЕМ-волны, они существуют на любой частоте.

Поэтому легко установить возможность существования ТЕМ-волн в линии передачи. Волна ТЕМ в линии существует, если эта линия может быть использована как линия постоянного тока.

Прежде рассматривались уравнения Гельмгольца в скалярном виде (6.1) и его применяли для отыскания продольных составляющих электромагнитного поля  и . Если записать уравнения Гельмгольца в векторном виде и положить в них , то получим при c = 0